Question

已知正三棱锥P-ABC的底面边长为6，侧棱长为

13

．有一动点M在侧面PAB内，它到顶点P的距离与到底面ABC的距离比为2

2

：1．

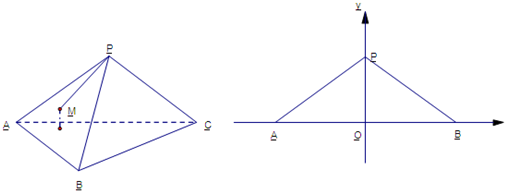
（1）求动点M到顶点P 的距离与它到边AB的距离之比；
（2）在侧面PAB所在平面内建立为如图所示的直角坐标系，求动点M的轨迹方程．

Answer 1

分析：（1）作PO⊥底面ABC于O点，则O为△ABC的中心，连接CO并延长交AB于D，连PD，则∠PDC为侧面与底面所成二面角的平面角，作MN⊥底面于N，作NQ⊥AB于Q，连MQ，则∠MQN为侧面与底面所成二面角的平面角，从而MQ=2MN，即可求出M到顶点P的距离与它到边AB的距离之比．
（2）设M点的坐标为（x，y），根据

|PM|

|MQ|

=

2

建立等式关系，求出点M的轨迹，然后求出x和y的范围，从而求出所求．

解答：解：

（1）作PO⊥底面ABC于O点，则O为△ABC的中心，连接CO并延长交AB于D，连PD，则∠PDC为侧面与底面所成二面角的平面角．∵AB=6，∴DO=

3

 ， PD=

PB2-BD2

=2∴∠PDO=30°----------------------------4′
作MN⊥底面于N，作NQ⊥AB于Q，连MQ，则∠MQN为侧面与底面所成二面角的平面角，∴∠MQN=30°．
于是，MQ=2MN，有题意

PM

MN

=2

2

：1，∴

PM

MQ

=

2

：1
即M到顶点P的距离与它到边AB的距离之比为

2

：1---------------------------8′
（2）设M点的坐标为（x，y），由

|PM|

|MQ|

=

2

，P（0，2）得：

x2+(y-2)2

|y|

=

2

，化简得：x²-y²-4y+4=0------12′
直线PB的方程为

x

3

+

y

2

=1，由

x2-y2-4y+4=0 x 3 + y 2 =1

，解得x=

-24+6 26

5

综上，M点的轨迹方程为x²-y²-4y+4=0(

24-6 26

5

≤x≤

-24+6 26

5

，y＞0)-----------------------14′

点评：本题主要考查了棱锥的结构特征以及轨迹方程，同时考查了计算能力和推理论证的能力，属于中档题．