Question

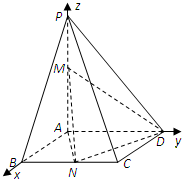在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥面ABCD，PA=2，点M，N分别为边PA，BC的中点．建立如图所示的直角坐标系A-xyz．
（1）求异面直线AN与MD所成角的余弦值；
（2）求点B到平面MND的距离．

Answer 1

分析：（1）建立空间直角坐标系，给出相关点的坐标，求出

AN

，

MD

的坐标表示，利用向量坐标运算求向量夹角的余弦值；
（2）利用正弦定理求△MND的面积，利用三棱锥的换底性，求B到平面MND的距离．

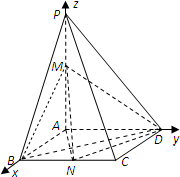
解答：解：（1）建立空间直角坐标系如图：
则A（0，0，0），B（1，0，0），D（0，1，0），C（1，1，0），N（1，

1

2

，0），M（0，0，1），
∴

AN

=（1，

1

2

，0）；

MD

=（0，1，-1）
cos＜

AN

，

MD

＞=

AN • MD

| AN || MD |

=

1 2

2 × 5 2

=

10

10

，
∴异面直线AN与MD所成角的余弦值为

10

10

．
（2）连接BD，MD，设点B到平面MND的距离为H，
MD=

2

，MN=

1+1+ 1 4

=

3

2

，DN=

1 4 +1

=

5

2

，
∴cos∠MDN=

2+ 5 4 - 9 4

2× 2 × 5 2

=

10

10

，
∴sin∠MDN=

3 10

10

，
S_△MDN=

1

2

×MD×ND×sin∠MDN=

1

2

×

2

×

5

2

×

3 10

10

=

3

4

．
V_B-MND=V_M-BDN⇒

1

3

×

3

4

×H=

1

3

×

1

2

×

1

2

×1×1⇒H=

1

3

．
∴点B到平面MND的距离为

1

3

．

点评：本题考查了向量法求异面直线所成角的余弦值，考查了利用三棱锥的换底性求点到平面的距离，解答本题的关键是利用正弦定理与余弦定理求△MND的面积，体现了转化思想．