题目内容
 在如图所示的直角坐标系中,B为单位圆在第一象限内圆弧上的动点,A(1,0),设∠AOB=x(0<x<
在如图所示的直角坐标系中,B为单位圆在第一象限内圆弧上的动点,A(1,0),设∠AOB=x(0<x<| π |
| 2 |
| ||
| 3 |
(1)求点C的坐标 (用含x的式子表示);
(2)试求△ABC的面积的最大值,并求出相应x值.
分析:(1)确定B的坐标,利用过B作直线BC∥OA,并交直线y=-
x于点C,可得点C的坐标;
(2)表示出△ABC的面积,利用辅助角公式化简,结合角的范围,即可得到结论.
| ||
| 3 |
(2)表示出△ABC的面积,利用辅助角公式化简,结合角的范围,即可得到结论.
解答: 解:(1)根据三角函数的定义,可知B(cosx,sinx)
解:(1)根据三角函数的定义,可知B(cosx,sinx)
∵BC∥OA
∴C点纵坐标为yC=sinx
将yC代入直线y=-
x,得:xC=-
sinx
∴点C(-
sinx,sinx);
(2)∵BC∥OA,
∴A到BC的距离为sinx
∵|BC|=cosx+
sinx
∴S△ABC=
|BC|sinx=
(cosx+
sinx)sinx=
sin(2x-
)+
∵0<x<
∴-
<2x-
<
∴当2x-
=
,即x=
时,S△ABC取得最大值为
+
.
 解:(1)根据三角函数的定义,可知B(cosx,sinx)
解:(1)根据三角函数的定义,可知B(cosx,sinx)∵BC∥OA
∴C点纵坐标为yC=sinx
将yC代入直线y=-
| ||
| 3 |
| 3 |
∴点C(-
| 3 |
(2)∵BC∥OA,
∴A到BC的距离为sinx
∵|BC|=cosx+
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
∵0<x<
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| 1 |
| 2 |
| ||
| 4 |
点评:本题考查利用数学知识解决实际问题,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
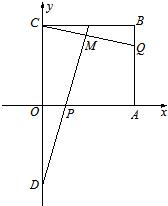 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,
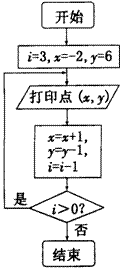
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,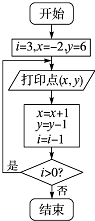 利用如图所示程序框图在直角坐标平面上打印一系列点,则打印的点落在坐标轴上的个数是( )
利用如图所示程序框图在直角坐标平面上打印一系列点,则打印的点落在坐标轴上的个数是( ) 本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.
本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分. (2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
(2012•大丰市一模)如图所示,在直角坐标平面内,反比例函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.