题目内容
对于三次函数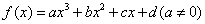 ,定义:设
,定义:设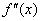 是函数
是函数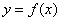 的导函数
的导函数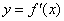 的导数,若
的导数,若 有实数解
有实数解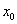 ,则称点
,则称点 为函数
为函数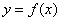 的“拐点”.已知函数
的“拐点”.已知函数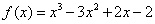 ,请解答下列问题:
,请解答下列问题:
(Ⅰ)求函数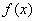 的“拐点”A的坐标;
的“拐点”A的坐标;
(Ⅱ)求证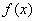 的图象关于“拐点”A对称,并写出对于任意三次函数都成立的有关“拐点”的一个结论(不需证明);
的图象关于“拐点”A对称,并写出对于任意三次函数都成立的有关“拐点”的一个结论(不需证明);
(Ⅲ)设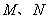 是函数
是函数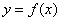 的两个极值点,求证:线段
的两个极值点,求证:线段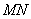 与曲线
与曲线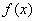 存在异于
存在异于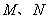 的共同点;
的共同点;
(Ⅳ)若另一个三次函数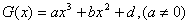 的“拐点”为
的“拐点”为 ,当
,当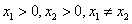 ,试比较
,试比较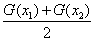 与
与 的大小.
的大小.
解:(Ⅰ)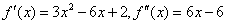
令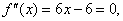 得
得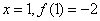
所以“拐点”A的坐标为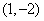
(Ⅱ)设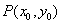 是
是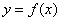 图象上任意一点,则
图象上任意一点,则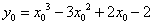
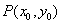 关于
关于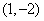 的对称点
的对称点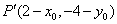 ,
,
把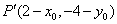 代入
代入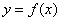 ,得左边
,得左边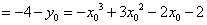
右边=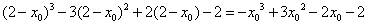
所以左边=右边,所以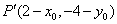 在
在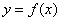 图象上,
图象上,
所以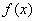 的图象关于“拐点”A对称.
的图象关于“拐点”A对称.
结论:任何三次函数的拐点都是它的对称中心(表达方式不唯一)
(Ⅲ)设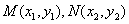 ,
,
因为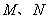 是函数
是函数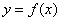 的两个极值点,所以
的两个极值点,所以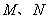 是
是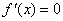 的两根,
的两根,
又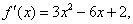 所以
所以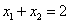
所以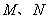 关于“拐点”A
关于“拐点”A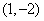 对称
对称
所以线段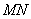 与曲线
与曲线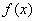 存在异于
存在异于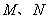 的共同点A
的共同点A
(Ⅳ)有题意知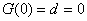 ,
,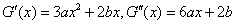
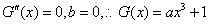
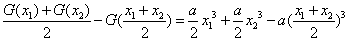
=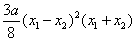
当 时,
时,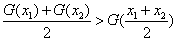 ,
,
当 时,
时,

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
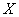 为停止取球后取球的次数,求
为停止取球后取球的次数,求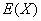 .
. 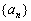 满足
满足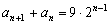 ,
,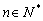 则数列
则数列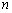 项和
项和 为
为 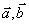 满足
满足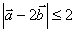 ,则
,则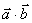 的最小值为( )
的最小值为( )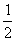 B.
B.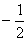 C.
C.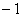 D.
D.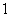
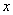 的不等式
的不等式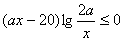 对任意的正整数
对任意的正整数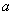 的取值范围为_____________.
的取值范围为_____________. ,
, ,
, ,……,
,……, (n∈N),则f2008(x) =( ).
(n∈N),则f2008(x) =( ). B.
B.  C.
C.  D.
D. 
 :变量X与变量Y没有关系.则在
:变量X与变量Y没有关系.则在 表示的意义是( )
表示的意义是( )


 满足
满足 (
( 为虚数单位),则
为虚数单位),则 为( )
为( )

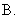

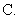

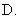
 [
[