题目内容

当x∈[
π
6
，
2π
3
]时，函数y=2sin(2x-
π
6
)-
m
2
有两个不同的零点，则实数m的范围是
[2，4）
[2，4）
．
分析：由x∈[
π
6
，
2π
3
]⇒2x-
π
6
∈[
π
6
，
7π
6
]⇒2sin（2x-
π
6
）∈[-1，2]，构造函数f（x）=2sin（2x-
π
6
），x∈[
π
6
，
2π
3
]，与函数g（x）=
m
2
，作图即可得实数m的范围．
解答：解：∵x∈[
π
6
，
2π
3
]，
∴2x-
π
6
∈[
π
6
，
7π
6
]，
∴2sin（2x-
π
6
）∈[-1，2]；
令f（x）=2sin（2x-
π
6
），x∈[
π
6
，
2π
3
]，
g（x）=
m
2
，
要使y=2sin（2x-
π
6
）-
m
2
有两个不同的零点，
则f（x）=2sin（2x-
π
6
），x∈[
π
6
，
2π
3
]与g（x）=
m
2
的图象有两个不同的交点，
作图如图
由图可知实数1≤
m
2
＜2，解得2≤m＜4．
故答案为：[2，4）．
点评：本题考查复合三角函数的单调性，考查函数的零点，着重考查数学结合思想与作图运算能力，属于中档题．
练习册系列答案
相关题目
已知函数f(x)=
sin4x+cos4x+sin2xcos2x
2-sin2x
-
1-cosx
4sin2
x
2

（1）判断函数f（x）的奇偶性．
（2）当x∈(
π
6
，
π
2
)时，求函数f（x）的值域．
（3）若
a
=(sinα，1)，
b
=(cosα，1)并且
a
∥
b
，求f（α）的值．
已知函数y=f（x）x∈[-π，
2π
3
]的图象关于直线x=-
π
6
对称，当x∈[-
π
6
，
2π
3
]时，函数f（x）=sin（ωx+?）（ω＞0，-
π
2
＜?＜
π
2
）的图象如图所示；
（1）求常数ω、?的值；
（2）求函数y=f（x）在[-π，
2π
3
]上的解析式；
（3）求方程f（x）=
2
2
的解集．
当x∈[-
π
6
，
2π
3
]时，函数f(x)=Asin(ωx+θ) (A＞0，ω＞0，|θ|＜
π
2
)的图象如图所示．
（1）求函数f（x）在[-
π
6
，
2π
3
]上的表达式；
（2）求方程f(x)=
2
2
在[-
π
6
，
2π
3
]的解集．
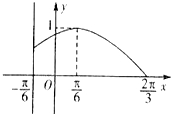精英家教网已知定义在区间[-π，
2
3
π]上的函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ≤π）的图象关于直线x=-
π
6
对称，当x∈[-
π
6
，
2π
3
]时，f（x）的图象如图所示．
（1）求f（x）在[-π，
2
3
π]上的表达式；
（2）求方程f（x）=
2
2
的解．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网