Question

已知函数y=f（x）x∈[-π，

2π

3

]的图象关于直线x=-

π

6

对称，当x∈[-

π

6

，

2π

3

]时，函数f（x）=sin（ωx+?）（ω＞0，-

π

2

＜?＜

π

2

）的图象如图所示；
（1）求常数ω、?的值；
（2）求函数y=f（x）在[-π，

2π

3

]上的解析式；
（3）求方程f（x）=

2

2

的解集．

Answer 1

分析：（1）由周期求出ω，由五点法作图求出φ的值．
（2）由方程可得-sinx=

2

2

，x∈[-π，-

π

6

）；或者 sin（x+

π

3

）=

2

2

，x∈[-

π

6

，

2π

3

]．解得x的值，即可求得方程的解集．

解答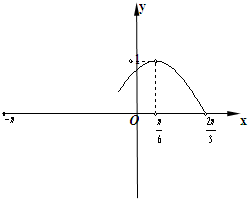：解：（1）由所给的图象可得

1

4

•

2π

ω

=

2π

3

-

π

6

，解得ω=1．
再由五点法作图可得1×

π

6

+?=

π

2

，解得 ?=

π

3

．…（4分）
（2）当x∈[-

π

6

，

2π

3

]时，函数f(x)=sin(x+

π

3

)
当x∈[-π，-

π

6

)时，-

π

3

-x∈(-

π

6

，

2π

3

]，f(x)=f(-

π

3

-x)=-sinx，x∈[-π，-

π

6

)．…（8分）
综上可得，f(x)=

-sinx (-π≤x＜- π 6 ) sin(x+ π 3 ) (- π 6 ≤x≤ 2π 3 )

．…（10分）
（3）f(x)=

2

2

，即-sinx=

2

2

，x∈[-π，-

π

6

）；或者 sin（x+

π

3

）=

2

2

，x∈[-

π

6

，

2π

3

]．
解得x=-

3π

4

，-

π

4

，-

π

12

，

5π

12

，
故方程的解集为{-

3π

4

，-

π

4

，-

π

12

，

5π

12

}．…（14分）

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，三角方程的解法，属于中档题．