题目内容
设函数f（x）=clnx+
x2+bx（b，c∈R，c≠0），且x=1为f（x）的极值点，
（Ⅰ）若x=1为f（x）的极大值点，求f（x）的单调区间（用c表示）；
（Ⅱ）若f（x）=0恰有1解，求实数c的取值范围。
x2+bx（b，c∈R，c≠0），且x=1为f（x）的极值点，（Ⅰ）若x=1为f（x）的极大值点，求f（x）的单调区间（用c表示）；
（Ⅱ）若f（x）=0恰有1解，求实数c的取值范围。
解：
，
因为x=1为f（x）的极值点，所以
，
所以
，
（Ⅰ）因为x=1为f（x）的极大值点，所以c＞1，
当
；
所以f（x）的递增区间为（0，1），（c，+∞）；递减区间为（1，c）。
（Ⅱ）若c＜0，则f（x）在（0，1）上递减，在（1，+∞）上递增，
f（x）=0恰有1解，
则
；
若0＜c＜1，
则
，
因为b=-1-c，
则
，
，
从而f（x）=0恰有一解；
若c＞1，
则
，
，
从而f（x）=0恰有一解；
所以所求c的范围为
。
，因为x=1为f（x）的极值点，所以
，所以
，（Ⅰ）因为x=1为f（x）的极大值点，所以c＞1，
当
；所以f（x）的递增区间为（0，1），（c，+∞）；递减区间为（1，c）。
（Ⅱ）若c＜0，则f（x）在（0，1）上递减，在（1，+∞）上递增，
f（x）=0恰有1解，
则
；若0＜c＜1，
则
，因为b=-1-c，
则
，，从而f（x）=0恰有一解；
若c＞1，
则
，，从而f（x）=0恰有一解；
所以所求c的范围为
。
练习册系列答案
相关题目
。
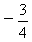