题目内容
设函数f(x)=clnx+
x2+bx(b,c∈R,c≠0),且x=1为f(x)的极值点.
(Ⅰ)若x=1为f(x)的极大值点,求f(x)的单调区间(用c表示);
(Ⅱ)若f(x)=0恰有两解,求实数c的取值范围.
| 1 | 2 |
(Ⅰ)若x=1为f(x)的极大值点,求f(x)的单调区间(用c表示);
(Ⅱ)若f(x)=0恰有两解,求实数c的取值范围.
分析:(Ⅰ利用x=1为f(x)的极大值点,得到f'(1)=0,然后利用导数研究f(x)的单调区间(用c表示);
(Ⅱ)分别讨论c的取值,讨论极大值和极小值之间的关系,从而确定c的取值范围.
(Ⅱ)分别讨论c的取值,讨论极大值和极小值之间的关系,从而确定c的取值范围.
解答:解:f′(x)=
+x+b=
,
∵x=1为f(x)的极值点,
∴f'(1)=0,
∴f′(x)=
且c≠1,b+c+1=0.
(I)若x=1为f(x)的极大值点,
∴c>1,
当0<x<1时,f'(x)>0;
当1<x<c时,f'(x)<0;
当x>c时,f'(x)>0.
∴f(x)的递增区间为(0,1),(c,+∞);递减区间为(1,c).
(II)①若c<0,则f(x)在(0,1)上递减,在(1,+∞)上递增,
f(x)=0恰有两解,则f(1)<0,即
+b<0,∴-
<c<0;
②若0<c<1,则f极大(x)=f(c)=clnc+
c2b+c,
f 极小(x)=f(1)=
+b,
∵b=-1-c,
则f极大(x)=clnc+
c2+c(-1-c)=clnc-c-
c2<0,
f 极小(x)=-
-c,从而f(x)=0只有一解;
③若c>1,则f极小(x)=clnc+
c2+c(-1-c)=clnc-c-
c2<0,
f极大(x)=-
-c,则f(x)=0只有一解.
综上,使f(x)=0恰有两解的c的范围为:-
<c<0.
| c |
| x |
| x2+bx+c |
| x |
∵x=1为f(x)的极值点,
∴f'(1)=0,
∴f′(x)=
| (x-1)(x-c) |
| x |
(I)若x=1为f(x)的极大值点,
∴c>1,
当0<x<1时,f'(x)>0;
当1<x<c时,f'(x)<0;
当x>c时,f'(x)>0.
∴f(x)的递增区间为(0,1),(c,+∞);递减区间为(1,c).
(II)①若c<0,则f(x)在(0,1)上递减,在(1,+∞)上递增,
f(x)=0恰有两解,则f(1)<0,即
| 1 |
| 2 |
| 1 |
| 2 |
②若0<c<1,则f极大(x)=f(c)=clnc+
| 1 |
| 2 |
f 极小(x)=f(1)=
| 1 |
| 2 |
∵b=-1-c,
则f极大(x)=clnc+
| 1 |
| 2 |
| 1 |
| 2 |
f 极小(x)=-
| 1 |
| 2 |
③若c>1,则f极小(x)=clnc+
| 1 |
| 2 |
| 1 |
| 2 |
f极大(x)=-
| 1 |
| 2 |
综上,使f(x)=0恰有两解的c的范围为:-
| 1 |
| 2 |
点评:本题主要考查利用导数研究函数的极值和单调性,考查学生的计算能力,以及分类讨论思想.

练习册系列答案
相关题目
 x2+bx(b,c∈R,c≠0),且x=1为f(x)的极值点,
x2+bx(b,c∈R,c≠0),且x=1为f(x)的极值点,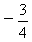 。
。