Question

【题目】已知函数.

（1）用“五点法”作函数的图象；

（2）说出此图象是由的图象经过怎样的变化得到的；

（3）求此函数的对称轴、对称中心、单调递增区间.

Answer 1

【答案】（1）见解析；（2）见解析；（3）对称轴，；对称中心，；单调递增区间，.

【解析】

（1）根据五点作图法列出表格，找出五点的坐标，在平面直角坐标系中画出图象即可；

（2）由三角函数图象平移变换过程，即可得由的图象得到的过程；

（3）根据正弦函数的图象与性质，即可由整体代入法分别求得的对称轴、对称中心、单调递增区间.

（1）函数，对应五点如下表所示：

将点坐标分别描在平面直角坐标系中，连接各点如下图所示：

，

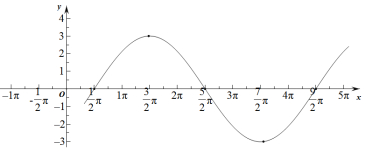（2）方法一：将的横坐标扩大为原来的2倍，可得，再将函数图象向右平移个单位可得，最后将纵坐标伸长为原来的倍，即可得；

方法二：将向右平移个单位可得，再将横坐标扩大为原来的2倍，可得，最后将纵坐标伸长为原来的倍，即可得；

（3）由正弦函数的图象与性质可知，函数对称轴满足，解得，；

由正弦函数的图象与性质可知，函数对称中心满足，解得，所以对称中心为，；

由正弦函数的图象与性质可知，函数的单调递增区间满足，解得，所以单调递增区间为，.