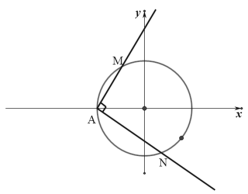
题目内容
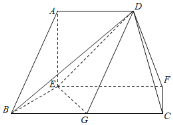
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求二面角C-DF-E的余弦值.
【答案】(Ⅰ)![]() ∴四边形
∴四边形![]() 是平行四边形∴
是平行四边形∴![]() ∴
∴![]() 平面
平面![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题(Ⅰ)利用判定定理证明线面平行时,关键是在平面内找一条与已知直线平行的直线,解题时可先直观判断平面内是否已有,若没有,则需作出该直线,常考虑三角形的中位线、平行四边形的对边或过平行线分线段成比例等;(Ⅱ)1.使用空间向量求解空间角的关键是建立空间直角坐标系后,将空间角转化为向量的运算,然后借助于直线的方向向量和平面的法向量解决立体几何中的计算问题.在角的问题中,线面角和二面角是重点.2.注意角的范围,如异面直线所成角的范围是![]() ,线面角的范围是
,线面角的范围是![]() ,二面角的范围是
,二面角的范围是![]() .
.
试题解析:(Ⅰ)证明:∵![]() ,∴
,∴![]() .
.
又∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() . 2分
. 2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() . 4分
. 4分
(Ⅱ)解∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 两两垂直.
两两垂直.
以点E为坐标原点,以![]() 所在直线分别为
所在直线分别为![]() 轴建立如图的空间直角坐标系. 6分
轴建立如图的空间直角坐标系. 6分
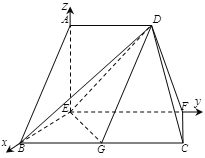
由已知得,![]() (0,0,2),
(0,0,2),![]() (2,0,0),
(2,0,0),
![]() (2,4,0),
(2,4,0),![]() (0,3,0),
(0,3,0),![]() (0,2,2). 7分
(0,2,2). 7分
由已知得![]() 是平面
是平面![]() 的法向量. 8分
的法向量. 8分
设平面![]() 的法向量为
的法向量为![]() ,
,
∵![]() ,
,
∴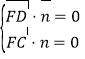 ,即
,即![]() ,令
,令![]() ,得
,得![]() . 10分
. 10分
设二面角![]() 的大小为
的大小为![]() ,由图知
,由图知![]() 为钝角,
为钝角,
∴![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() 12分
12分

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目