题目内容
11、在R上定义运算?:x?y=x(1-y),若不等式(x-a)?(x+1)≥1无解,则实数a的取值范围
-2<a<2
.分析:由在R上定义运算?:x?y=x(1-y),把(x-a)?(x+1)=(x-a)(-x),转化为一元二次不等式)(x-a)(-x)≥1无解,应用判别式即可求得结果.
解答:解:∵x?y=x(1-y),
∴(x-a)?(x+1)≥1无解?-x(x-a)≥1无解
即-x2+ax-1≥0无解.
∴△=a2-4<0,解得-2<a<2.
故答案为:-2<a<2.
∴(x-a)?(x+1)≥1无解?-x(x-a)≥1无解
即-x2+ax-1≥0无解.
∴△=a2-4<0,解得-2<a<2.
故答案为:-2<a<2.
点评:此题的难点在于能否对于给定的定义理解透彻,也是此题新意,能有效考查学生灵活应用知识分析、解决问题的能力.这个的立意很好,属中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 :x
:x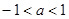 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.