题目内容
.函数 是
是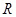 上的可导函数,
上的可导函数,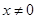 时,
时, ,则函数
,则函数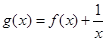 的零点个数为( )
的零点个数为( )
A.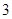 | B.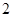 | C.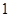 | D. |
D
解析试题分析:由于函数g(x)=f(x)+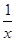 ,可得x≠0,因而 g(x)的零点跟 xg(x)的非零零点是完全一样的,故我们考虑 xg(x)=xf(x)+1 的零点.由于当x≠0时,f′(x)+
,可得x≠0,因而 g(x)的零点跟 xg(x)的非零零点是完全一样的,故我们考虑 xg(x)=xf(x)+1 的零点.由于当x≠0时,f′(x)+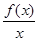 >0,
>0,
①当x>0时,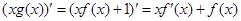 =
=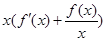 >0,所以
>0,所以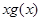 在(0,+∞)上是单调递增函数.又∵
在(0,+∞)上是单调递增函数.又∵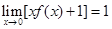 ,∴当x∈(0,+∞)时,函数
,∴当x∈(0,+∞)时,函数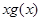 =
=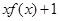 >1恒成立,因此
>1恒成立,因此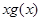 =
=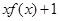 在(0,+∞)上没有零点.
在(0,+∞)上没有零点.
②当x<0时,由于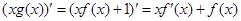 =
=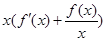 <0,
<0,
故函数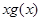 在(-∞,0)上是递减函数,函数
在(-∞,0)上是递减函数,函数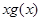 =
=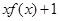 >1恒成立,
>1恒成立,
故函数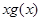 在(-∞,0)上无零点.
在(-∞,0)上无零点.
综上可得,函g(x)=f(x)+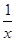 在R上的零点个数为0.
在R上的零点个数为0.
考点:函数与导数的关系,函数零点,转化思想

练习册系列答案
相关题目
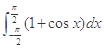 等于( )
等于( )
A.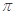 | B.2 | C.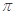 -2 -2 | D.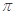 +2 +2 |
函数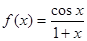 在
在 处的切线方程是( )
处的切线方程是( )
A. | B.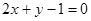 |
C.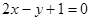 | D.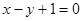 |
若点P是曲线y=x2-ln x上任意一点,则点P到直线y=x-2的最小值为( )
| A.1 | B. | C. | D. |
若函数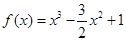 ,则( )
,则( )
A.最大值为 ,最小值为 ,最小值为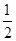 | B.最大值为 ,无最小值 ,无最小值 |
C.最小值为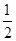 ,无最大值 ,无最大值 | D.既无最大值也无最小值 |
函数 在[0,3]上的最大值和最小值分别是
在[0,3]上的最大值和最小值分别是
| A.5,15 | B.5,-14 | C.5,-15 | D.5,-16 |
设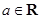 ,函数
,函数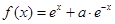 的导函数
的导函数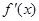 是奇函数,若曲线
是奇函数,若曲线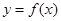 的一条切线的斜率是
的一条切线的斜率是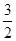 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.- | B.-ln2 | C. | D.ln2 |
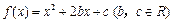 ,且
,且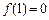 .
.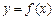 与x轴的两个交点
与x轴的两个交点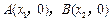 之间的距离为2,求b的值;
之间的距离为2,求b的值; 的两个实数根分别在区间
的两个实数根分别在区间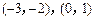 内,求b的取值范围.
内,求b的取值范围. 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象的大致形状是( )
的图象的大致形状是( ) 
