题目内容
函数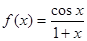 在
在 处的切线方程是( )
处的切线方程是( )
A. | B.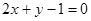 |
C.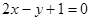 | D.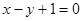 |
A
解析试题分析:∵ ,
,
∴切线的斜率 ,切点坐标(0,1)
,切点坐标(0,1)
∴切线方程为y-1=-(x-0),即x+y-1=0.
故选A.
考点:导数的几何意义;函数的求导运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数 在
在 处的切线方程是( )
处的切线方程是( )
A.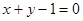 | B.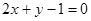 |
C. | D.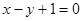 |
设函数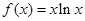 ,则
,则 的极小值点为( )
的极小值点为( )
A.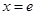 | B.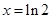 | C.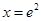 | D.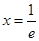 |
设函数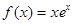 ,则( )
,则( )
A.x=1为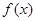 的极大值点 的极大值点 |
B.x=-1为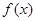 的极大值点 的极大值点 |
C.x=1为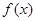 的极小值点 的极小值点 |
D.x=-1为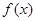 的极小值点 的极小值点 |
.函数 是
是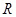 上的可导函数,
上的可导函数,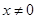 时,
时, ,则函数
,则函数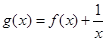 的零点个数为( )
的零点个数为( )
A.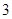 | B.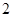 | C.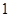 | D. |
下列各命题中,不正确的是( )
A.若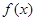 是连续的奇函数,则 是连续的奇函数,则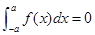 |
B.若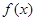 是连续的偶函数,则 是连续的偶函数,则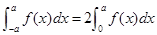 |
C.若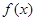 在 在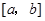 上连续且恒正,则 上连续且恒正,则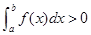 |
D.若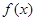 在 在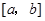 上连续,且 上连续,且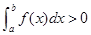 ,则 ,则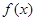 在 在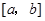 上恒正 上恒正 |
已知函数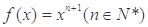 的图象与直线
的图象与直线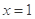 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为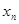 ,则
,则 +
+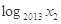 +…+
+…+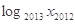 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
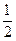 lg2+
lg2+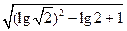 -
-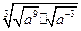 ÷
÷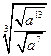 ;
;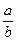 的值.
的值.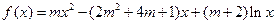 ,其中m为R上的常数,若函数
,其中m为R上的常数,若函数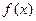 在x=1处取得极大值0,
在x=1处取得极大值0,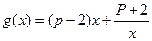 ,若对
,若对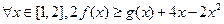 恒成立,
恒成立,