题目内容
(本题满分14分)在等差数列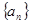 中,
中,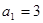 ,其前
,其前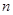 项和为
项和为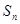 ,等比数列
,等比数列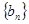 的各项均为正数,
的各项均为正数,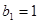 ,公比为
,公比为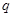 ,且
,且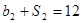 ,
, 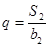 .
.
(Ⅰ)求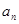 与
与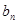 ;(Ⅱ)证明:
;(Ⅱ)证明: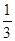 ≤
≤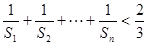 .
.
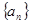 中,
中,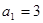 ,其前
,其前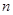 项和为
项和为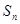 ,等比数列
,等比数列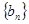 的各项均为正数,
的各项均为正数,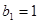 ,公比为
,公比为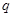 ,且
,且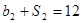 ,
, 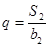 .
.(Ⅰ)求
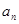 与
与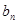 ;(Ⅱ)证明:
;(Ⅱ)证明: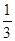 ≤
≤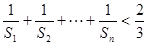 .
. (Ⅰ) ,
, .(Ⅱ)见解析。.
.(Ⅱ)见解析。.
 ,
, .(Ⅱ)见解析。.
.(Ⅱ)见解析。. 、本题考查数列的通项与求和,考查等差数列与等比数列的综合,考查裂项法求数列的和,属于中档题.
(1)根据b2+S2=12,{bn}的公比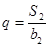 ,建立方程组,即可求出an与bn;
,建立方程组,即可求出an与bn;
(2)因为 ,
,
所以 ,然后裂项求和。
,然后裂项求和。
解:(Ⅰ)设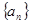 的公差为
的公差为 ,
,
因为 所以
所以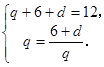
解得 或
或 (舍),
(舍), .
.
故 ,
, . ……………6分
. ……………6分
(Ⅱ)因为 ,
,
所以 . ………9分
. ………9分
故

 . ………11分
. ………11分
因为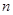 ≥
≥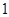 ,所以
,所以 ≤
≤ ,于是
,于是 ≤
≤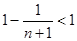 ,
,
所以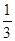 ≤
≤ .
.
即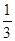 ≤
≤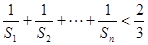 . …………14分
. …………14分
(1)根据b2+S2=12,{bn}的公比
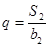 ,建立方程组,即可求出an与bn;
,建立方程组,即可求出an与bn;(2)因为
 ,
,所以
 ,然后裂项求和。
,然后裂项求和。解:(Ⅰ)设
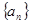 的公差为
的公差为 ,
,因为
 所以
所以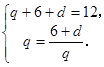
解得
 或
或 (舍),
(舍), .
.故
 ,
, . ……………6分
. ……………6分(Ⅱ)因为
 ,
,所以
 . ………9分
. ………9分故


 . ………11分
. ………11分因为
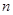 ≥
≥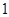 ,所以
,所以 ≤
≤ ,于是
,于是 ≤
≤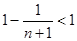 ,
,所以
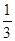 ≤
≤ .
.即
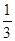 ≤
≤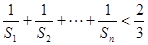 . …………14分
. …………14分
练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
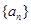 中,若
中,若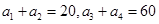 ,则
,则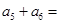 .
. 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.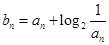 ,
, ,求使
,求使  成立的
成立的 的最小值.
的最小值. 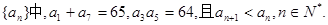
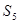 ;
;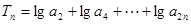 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值. 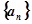 中,已知
中,已知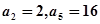 .
.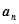 ;
;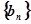 ,
,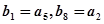 ,求数列
,求数列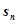 ,并求
,并求 为等比数列,且
为等比数列,且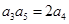 ,设等差数列
,设等差数列 的前
的前 项和为
项和为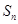 ,若
,若 ,则
,则
 的等差数列
的等差数列 的各项依次插入等比数列
的各项依次插入等比数列 中,将
中,将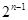 项的各组,得到数列
项的各组,得到数列 :b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若
:b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若 ,且
,且 ,则
,则 等于( )
等于( )

 各项均为正数,且
各项均为正数,且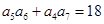 ,则
,则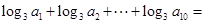
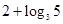
 ,有
,有 成立,
成立, ( )
( )