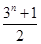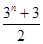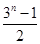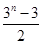题目内容
已知等比数列 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若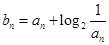 ,
, ,求使
,求使  成立的
成立的 的最小值.
的最小值.
 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若
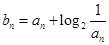 ,
, ,求使
,求使  成立的
成立的 的最小值.
的最小值. (Ⅰ)数列 的通项公式
的通项公式 .
.
(Ⅱ)使 成立的正整数
成立的正整数 的最小值为
的最小值为 .
.
 的通项公式
的通项公式 .
. (Ⅱ)使
 成立的正整数
成立的正整数 的最小值为
的最小值为 .
.本试题主要是考查了数列的通项公式的求解,以及数列求和的综合运用。
(1)因为等比数列 满足
满足 ,且
,且 是
是 ,
, 的等差中项,利用通项公式的性质可知结论。
的等差中项,利用通项公式的性质可知结论。
(2)因为 .然后利用分组求和法得到结论。
.然后利用分组求和法得到结论。
(1)因为等比数列
 满足
满足 ,且
,且 是
是 ,
, 的等差中项,利用通项公式的性质可知结论。
的等差中项,利用通项公式的性质可知结论。(2)因为
 .然后利用分组求和法得到结论。
.然后利用分组求和法得到结论。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
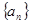 中,
中,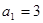 ,其前
,其前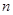 项和为
项和为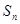 ,等比数列
,等比数列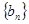 的各项均为正数,
的各项均为正数,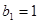 ,公比为
,公比为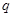 ,且
,且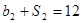 ,
, 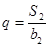 .
.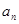 与
与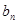 ;(Ⅱ)证明:
;(Ⅱ)证明: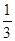 ≤
≤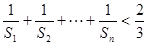 .
. 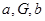 成等比"是"
成等比"是"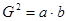 "的 条件( )
"的 条件( )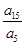 =( )
=( )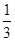
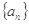 的前
的前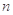 项和
项和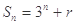 ,则
,则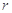 = ( )
= ( )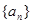 满足:
满足: 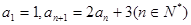 ,则
,则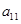 =( )
=( )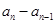 ,…是首项为1,公比为3的等比数列,则an等于( )
,…是首项为1,公比为3的等比数列,则an等于( )