题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.
(1)求证:a,b,c成等差数列;
(2)若C= ,求
,求 的值.
的值.
[解析] (1)由已知得sinAsinB+sinBsinC=2sin2B,
因为sinB≠0,所以sinA+sinC=2sinB.
由正弦定理,有a+c=2b,即a,b,c成等差数列.
(2)由C= ,c=2b-a及余弦定理得
,c=2b-a及余弦定理得
(2b-a)2=a2+b2+ab,
即有5ab-3b2=0,所以 =
= .
.

练习册系列答案
相关题目
铁矿石A和B的含铁率为a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c,如下表:
|
| a | b(万吨) | c( 百万元) |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).
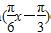 (0≤x≤9)的最大值与最小值之和为( )
(0≤x≤9)的最大值与最小值之和为( )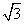 B.0
B.0
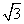 ,∠A=
,∠A= ,则∠C的大小为________.
,则∠C的大小为________. 的取值范围是( )
的取值范围是( )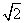 ,2) D.(
,2) D.( m B.20
m B.20 m
m )m D.30m
)m D.30m 米 B.10
米 B.10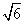 米
米 米 D.20
米 D.20 米
米