题目内容
(本小题满分14分)已知椭圆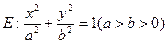 的左、右焦点分别为
的左、右焦点分别为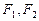 ,点
,点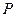 是
是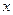 轴上方椭圆
轴上方椭圆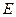 上的一点,且
上的一点,且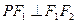 ,
, 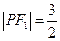 ,
, 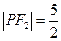 .
.
(Ⅰ)求椭圆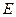 的方程和
的方程和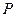 点的坐标;
点的坐标;
(Ⅱ)判断以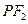 为直径的圆与以椭圆
为直径的圆与以椭圆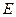 的长轴为直径的圆的位置关系;
的长轴为直径的圆的位置关系;
(Ⅲ)若点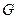 是椭圆
是椭圆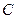 :
: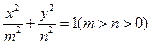 上的任意一点,
上的任意一点,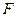 是椭圆
是椭圆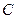 的一个焦点,探究以
的一个焦点,探究以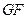 为直径的圆与以椭圆
为直径的圆与以椭圆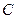 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.
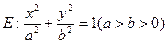 的左、右焦点分别为
的左、右焦点分别为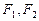 ,点
,点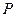 是
是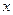 轴上方椭圆
轴上方椭圆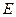 上的一点,且
上的一点,且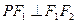 ,
, 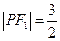 ,
, 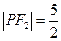 .
.(Ⅰ)求椭圆
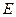 的方程和
的方程和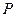 点的坐标;
点的坐标;(Ⅱ)判断以
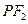 为直径的圆与以椭圆
为直径的圆与以椭圆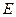 的长轴为直径的圆的位置关系;
的长轴为直径的圆的位置关系;(Ⅲ)若点
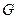 是椭圆
是椭圆 :
: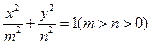 上的任意一点,
上的任意一点, 是椭圆
是椭圆 的一个焦点,探究以
的一个焦点,探究以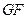 为直径的圆与以椭圆
为直径的圆与以椭圆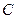 的长轴为直径的圆的位置关系.
的长轴为直径的圆的位置关系.(Ⅰ) ,
,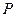
 ;
;
(Ⅱ)两圆相切;
(Ⅲ)两圆内切。
 ,
,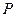
 ;
;(Ⅱ)两圆相切;
(Ⅲ)两圆内切。
(Ⅰ) 在椭圆
在椭圆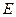 上
上 , …………….1分
, …………….1分
 ,
, ……………….2分[
……………….2分[
 ,
,  .
.
所以椭圆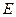 的方程是:
的方程是: ……………….4分
……………….4分

 ,
,
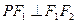
 ……….5分
……….5分
(Ⅱ)线段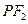 的中点
的中点
∴以 为圆心
为圆心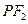 为直径的圆
为直径的圆 的方程为
的方程为
圆 的半径
的半径 …………….8分
…………….8分

 ,以椭圆
,以椭圆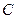 的长轴为直径的圆
的长轴为直径的圆 的半径
的半径 ,
,
两圆圆心 、
、 分别是
分别是 和
和 的中点,
的中点,
∴两圆心间的距离 ,所以两圆内切.…….14分
,所以两圆内切.…….14分
 在椭圆
在椭圆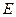 上
上 , …………….1分
, …………….1分 ,
, ……………….2分[
……………….2分[ ,
,  .
. 所以椭圆
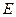 的方程是:
的方程是: ……………….4分
……………….4分
 ,
,
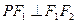
 ……….5分
……….5分(Ⅱ)线段
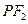 的中点
的中点
∴以
 为圆心
为圆心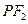 为直径的圆
为直径的圆 的方程为
的方程为
圆
 的半径
的半径 …………….8分
…………….8分
 ,以椭圆
,以椭圆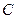 的长轴为直径的圆
的长轴为直径的圆 的半径
的半径 ,
,两圆圆心
 、
、 分别是
分别是 和
和 的中点,
的中点,∴两圆心间的距离
 ,所以两圆内切.…….14分
,所以两圆内切.…….14分
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
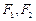 分别是椭圆
分别是椭圆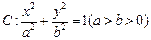 的左、右焦点,过
的左、右焦点,过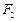 的直线
的直线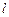 与椭圆
与椭圆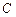 相交于A,B两点,直线
相交于A,B两点,直线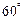 ,
,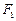 到直线
到直线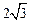 .
.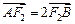 ,求椭圆
,求椭圆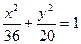 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于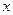 轴上方,
轴上方,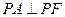 .
.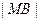 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离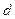 的最小值.
的最小值.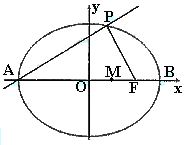
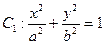 的左、右两个焦点分别为F1、F2,离心率为
的左、右两个焦点分别为F1、F2,离心率为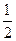 ,且抛物线
,且抛物线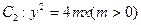 与椭圆C1有公共焦点F2(1,0)。
与椭圆C1有公共焦点F2(1,0)。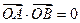 ,过原点O作直线AB的垂线OD,垂足为D,求点D为轨迹方程。
,过原点O作直线AB的垂线OD,垂足为D,求点D为轨迹方程。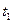 时刻测得它的影长为4米,在
时刻测得它的影长为4米,在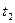 时刻的影长为1米。这个广场上有一个球形物体,它在地面上的影子是椭圆,问在
时刻的影长为1米。这个广场上有一个球形物体,它在地面上的影子是椭圆,问在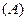 1:1
1:1 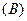
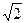 :1
:1 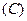
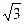 :1
:1 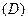 2:1
2:1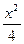 +y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,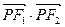 的值为 ( )
的值为 ( )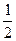
 ,右焦点F(c,0),方程
,右焦点F(c,0),方程 的两个根分别为x1,x2,则点P(x1,x2)在
的两个根分别为x1,x2,则点P(x1,x2)在 内
内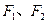 分别为椭圆
分别为椭圆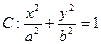 (
(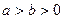 )的左、右焦点,过F2的
)的左、右焦点,过F2的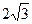 .
.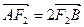 ,求椭圆C的方程.
,求椭圆C的方程.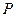 满足
满足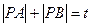 ,若P点的轨迹是椭圆,则
,若P点的轨迹是椭圆,则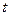 的取值范围是
的取值范围是 。
。