题目内容
(本题满分10分)选修4—1:几何证明选讲.
已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.

(Ⅰ)求∠BAE 的度数;
(Ⅱ)求证: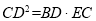
(Ⅰ) 见解析;(Ⅱ) 见解析
【解析】
试题分析:(Ⅰ)在△EAB与△ECA中,因为AE为圆O的切线,所以∠EBA =∠EAC,∠EAB =∠ECA,因为△ACD为等边三角形,所以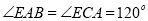 ;(Ⅱ)容易证明△ABD∽△EAC ,所以
;(Ⅱ)容易证明△ABD∽△EAC ,所以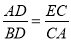 ,即
,即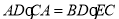 ,因为△ACD为等边三角形,所以AD=AC=CD, 所以
,因为△ACD为等边三角形,所以AD=AC=CD, 所以
试题解析:证明:(Ⅰ)在△EAB与△ECA中
因为AE为圆O的切线,所以∠EBA =∠EAC
又∠E公用,所以∠EAB =∠ECA
因为△ACD为等边三角形,所以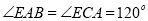 5分
5分
(Ⅱ)因为AE为圆O的切线,所以∠ABD=∠CAE
因为△ACD为等边三角形,所以∠ADC =∠ACD,
所以∠ADB=∠ECA,所以△ABD∽△EAC
所以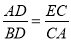 ,即
,即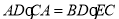
因为△ACD为等边三角形,所以AD=AC=CD,
所以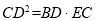 10分
10分
考点:平面几何的证明
考点分析: 考点1:几何证明选讲 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 中,
中, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
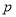 :存在
:存在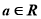 ,曲线
,曲线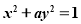 为双曲线;命题
为双曲线;命题 :
: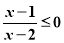 的解集是
的解集是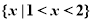 .给出下列结论中正确的有( )
.给出下列结论中正确的有( )
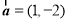 ,
,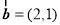 ,
,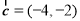 ,则下列说法中错误的是( )
,则下列说法中错误的是( )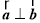
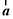 与向量
与向量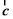 的夹角为
的夹角为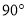
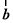 ∥
∥
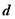 ,都存在一对实数
,都存在一对实数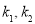 ,使得
,使得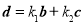
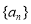 是一个单调递增的等差数列,且满足
是一个单调递增的等差数列,且满足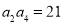 ,
,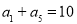 ,数列
,数列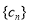 的前
的前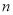 项和为
项和为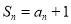
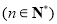 ,数列
,数列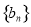 满足
满足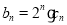 .
.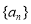 的通项公式;(Ⅱ)求数列
的通项公式;(Ⅱ)求数列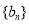 的前
的前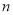 项和.
项和.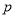 :存在
:存在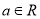 ,曲线
,曲线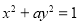 为双曲线;命题
为双曲线;命题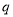 :
: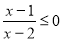 的解集是
的解集是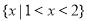 .给出下列结论中正确的有( )
.给出下列结论中正确的有( )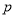 且
且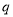 ”是真命题;
”是真命题;
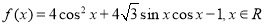 .
.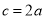 ,求
,求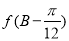 的值.
的值.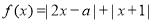 .
.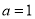 时,解不等式
时,解不等式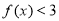 ;
;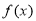 的最小值为1,求a的值.
的最小值为1,求a的值.