题目内容
(本小题满分10分)选修4-5:不等式选讲
已知函数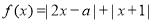 .
.
(Ⅰ)当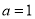 时,解不等式
时,解不等式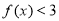 ;
;
(Ⅱ)若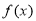 的最小值为1,求a的值.
的最小值为1,求a的值.
(1){x|-1<x<1};(2)a=-4或0.
【解析】
试题分析:本题主要考查不等式的证明、绝对值不等式的解法、不等式的性质等基础知识,意在考查考生的分析问题解决问题的能力、运算求解能力. 第一问,先利用零点分段法去掉绝对值,得到关于 的分段函数,再分别解
的分段函数,再分别解 的不等式,综合所得不等式;第二问,利用不等式的性质
的不等式,综合所得不等式;第二问,利用不等式的性质 ,关键是等号成立的条件必须同时成立,得到最小值
,关键是等号成立的条件必须同时成立,得到最小值 ,令其等于1,解绝对值不等式即可得到a的值.
,令其等于1,解绝对值不等式即可得到a的值.
试题解析:(Ⅰ)因为f(x)=|2x-1|+|x+1|= ,
,
且f(1)=f(-1)=3,所以,f(x)<3的解集为{x|-1<x<1}; 4分
(Ⅱ)|2x-a|+|x+1|=|x- |+|x+1|+|x-
|+|x+1|+|x- |≥|1+
|≥|1+ |+0=|1+
|+0=|1+ |
|
当且仅当(x+1)(x- )≤0且x-
)≤0且x- =0时,取等号.
=0时,取等号.
所以|1+ |=1,解得a=-4或0. 10分
|=1,解得a=-4或0. 10分
考点:不等式的证明、绝对值不等式的解法、不等式的性质.
考点分析: 考点1:含绝对值的不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目

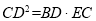
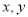 是两个实数,则“
是两个实数,则“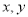 中至少有一个数大于1”是“
中至少有一个数大于1”是“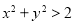 ”成立的( )
”成立的( ) ,
, .定义:
.定义: ,
, ,……,
,……, ,
, …满足
…满足 的点
的点 称为
称为 的n阶不动点.则
的n阶不动点.则 的n阶不动点的个数是( )
的n阶不动点的个数是( ) 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
 ;
; ,求四棱锥
,求四棱锥 的体积.
的体积. 分别与曲线
分别与曲线 ,
, 交于A,B,则
交于A,B,则 的最小值为( )
的最小值为( ) D.
D.
 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值. 上任意一点到两焦点
上任意一点到两焦点 距离之和为
距离之和为 ,离心率为
,离心率为 ,动点
,动点 在直线
在直线 上,过
上,过 作直线
作直线 的垂线
的垂线 ,设
,设 交椭圆于
交椭圆于 点.
点. 的标准方程;
的标准方程; 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;