题目内容
已知圆系方程x2+y2-4rxcosθ+4rysinθ-5r2=0(r为定值).(1)求此圆系表示的圆的圆心的轨迹方程;
(2)与圆系中所有的圆相切的圆是否存在,若存在,试求之.
解:(1)设圆心为M(x,y),则![]() (θ为参数),消去θ,得x2+y2=4r2,此为圆心的轨迹方程.
(θ为参数),消去θ,得x2+y2=4r2,此为圆心的轨迹方程.
(2)圆系方程为(x-2rcosθ)2+(y+2rsinθ)2=9r2.
∵3r+2r=5r及3r-2r=r,
∴与所有圆都相切的圆存在,其方程为x2+y2=25r2及x2+y2=r2.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
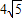 ?如果存在,试求直线l的方程;如果不存在,请说明理由.
?如果存在,试求直线l的方程;如果不存在,请说明理由.