题目内容
已知圆系方程x2+y2-2ax+2(a-2)y+2=0,其中a≠1,且a∈R,求证:该圆系恒过定点.
答案:
解析:
解析:
|
≠≠ 证法一:将此圆系变形,得到方程a(2y-2x)+x2+y2-4y+2=0,设其恒过定点(x1,y1),这意味着不论a为何值都有a(2y1-2x1)+x21+y21-4y1+2=0成立,它等价于方程组 证法二:取a=0,得x2+y2-4y+2=0,① 取a=2,得x2+y2-4x+2=0.② ①-②,得y=x,代入①得 将(1,1)代入x2+y2-2ax+2(a-2)y+2=0,得 12+12-2a+2(a-2)+2=2-2a+2a-4+2=0恒成立. 所以a取不为1的任意实数时,上述圆系恒过定点(1,1). 解析:对求这种含参变量(如本题中的a)方程恒过的定点的问题,一般的办法是将这个含参变量分离出来后通过讨论其恒过的定点所需满足的条件求解.还有一种办法就是将a取两个特殊值,得两个圆的方程,求其交点,必为所求的定点,求出交点坐标后,只需再验证即可.需要注意的是:当求到定点后,必须再代入方程进行一次检验.只有这样才能表示圆系对所有的a≠1,且a∈R恒过定点.题目要求a≠1是因为a=1时圆系方程代表一个点. |

练习册系列答案
相关题目
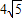 ?如果存在,试求直线l的方程;如果不存在,请说明理由.
?如果存在,试求直线l的方程;如果不存在,请说明理由.