题目内容
已知圆系方程x2+y2+2kx+(4k+10)y+5k2+20k=0(k∈R),是否存在斜率为2的直线l被圆系方程表示的任意一圆截得的弦长是定值4
?如果存在,试求直线l的方程;如果不存在,请说明理由.
| 5 |
(本小题满分14分)
假设存在满足条件的直线方程为y=2x+m,
圆的方程配方可得:(x+k)2+(y+2k+5)2=25.
所以圆心到直线的距离d=
|-2k+2k+5+m|=
,
由垂径定理可得:(
)2=52-(2
)2,
解得m=0或m=-10,
故存在满足条件的直线方程,方程为y=2x或y=2x-10.
假设存在满足条件的直线方程为y=2x+m,
圆的方程配方可得:(x+k)2+(y+2k+5)2=25.
所以圆心到直线的距离d=
| 1 | ||
|
| |5+m| | ||
|
由垂径定理可得:(
| |5+m| | ||
|
| 5 |
解得m=0或m=-10,
故存在满足条件的直线方程,方程为y=2x或y=2x-10.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
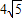 ?如果存在,试求直线l的方程;如果不存在,请说明理由.
?如果存在,试求直线l的方程;如果不存在,请说明理由.