题目内容
(本题14分)已知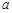 为实数,函数
为实数,函数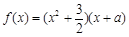 .
.
(I)若函数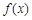 的图象上有与
的图象上有与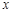 轴平行的切线,求
轴平行的切线,求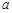 的取值范围;
的取值范围;
(II)若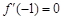 ,
,
(ⅰ) 求函数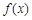 的单调区间;
的单调区间;
(ⅱ) 证明对任意的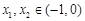 ,不等式恒成立。
,不等式恒成立。
【答案】
(I)实数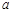 的取值范围是
的取值范围是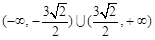
(ⅰ)函数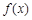 的单调增区间为
的单调增区间为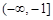 ,
,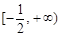 ;
;
单调减区间为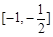 .
.
(ⅱ)任意的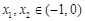 ,恒有
,恒有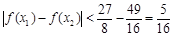 .
.
【解析】解:(Ⅰ) ∵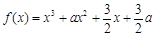 ,∴
,∴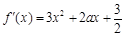 .……………2分
.……………2分
∵函数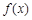 的图象上有与
的图象上有与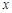 轴平行的切线,∴
轴平行的切线,∴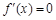 有实数解.
有实数解.
∴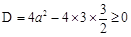 ,…………………4分
,…………………4分
∴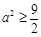 .因此,所求实数
.因此,所求实数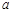 的取值范围是
的取值范围是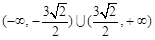 .……6分
.……6分
(Ⅱ) (ⅰ)∵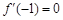 ,∴
,∴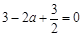 ,即
,即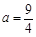 .
.
∴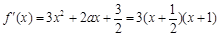 .
.
由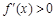 ,得
,得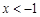 或
或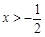 ; 由
; 由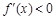 ,得
,得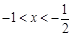 .
.
因此,函数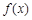 的单调增区间为
的单调增区间为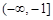 ,
,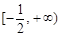 ;
;
单调减区间为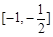 .………………………10分
.………………………10分
(ⅱ)由(ⅰ)的结论可知,
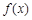 在
在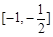 上的最大值为
上的最大值为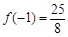 ,最小值为
,最小值为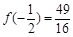 ;
;
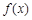 在
在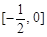 上的的最大值为
上的的最大值为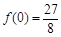 ,最小值为
,最小值为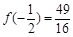 .
.
∴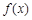 在
在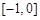 上的的最大值为
上的的最大值为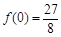 ,最小值为
,最小值为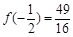 .
.
因此,任意的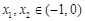 ,恒有
,恒有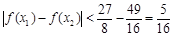 .………14分
.………14分

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
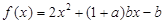 .
.
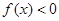 的解集为
的解集为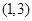 ,求实数
,求实数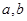 的值;
的值;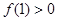 ,求满足条件的a的范围.
,求满足条件的a的范围.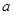 为实数,x=4是函数f(x)=alnx+x2-12x的一个极值点.
为实数,x=4是函数f(x)=alnx+x2-12x的一个极值点.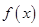 的单调区间;(Ⅲ)若直线
的单调区间;(Ⅲ)若直线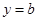 与函数
与函数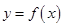 的图象有3个交点,求
的图象有3个交点,求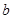 的取值范围.
的取值范围. 为常数,且
为常数,且 ,函数
,函数 ,
, (
( ,为自然对数的底数)
,为自然对数的底数) 的值;
的值; 的单调区间;
的单调区间; 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( ,直线
,直线 与曲线
与曲线 (
( )都有公共点?若存在,求出最小的实数
)都有公共点?若存在,求出最小的实数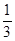 )是函数
)是函数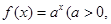 且
且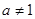 )的图象上一点,等比数列
)的图象上一点,等比数列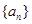 的前
的前 项和为
项和为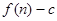 ,数列
,数列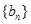
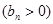 的首项为
的首项为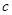 ,且前
,且前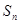 满足
满足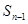 =
=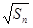 +
+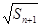 (
(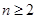 ).
).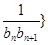 前
前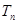 ,问
,问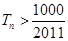 的最小正整数
的最小正整数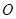 为坐标原点,
为坐标原点,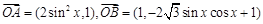 ,
,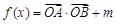 .
.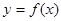 的单调递增区间;
的单调递增区间;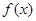 的定义域为
的定义域为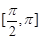 ,值域为
,值域为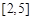 ,求
,求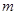 的值.
的值.