题目内容
(本题14分)已知点(1,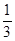 )是函数
)是函数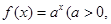 且
且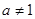 )的图象上一点,等比数列
)的图象上一点,等比数列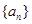 的前
的前 项和为
项和为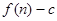 ,数列
,数列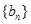
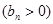 的首项为
的首项为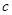 ,且前
,且前 项和
项和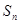 满足
满足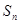 -
-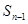 =
=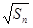 +
+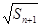 (
(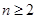 ).
).
(1)求数列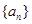 和
和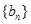 的通项公式;
的通项公式;
(2)若数列{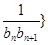 前
前 项和为
项和为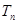 ,问
,问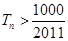 的最小正整数
的最小正整数 是多少? .
是多少? .
【答案】
解:(1)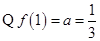 ,∴
,∴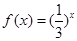 而
而
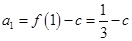 ,
,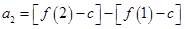
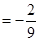 ,
,
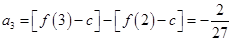 .
.
又数列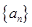 成等比数列,
成等比数列,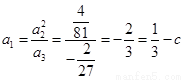 ,∴
,∴ 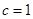 ;
;
从而公比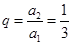 ,∴
,∴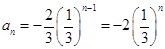 (
( 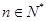 ) ;
) ;
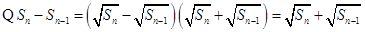

又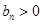 ,
,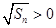 , ∴
, ∴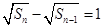 (
(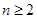 )
)
∴数列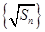 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列, ,
, 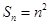
当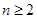 ,
, 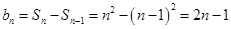 ;
;
∴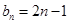 (
(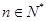 );
);
(2)
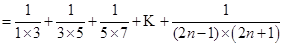
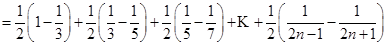
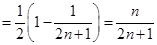 ;
;
由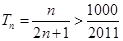 得
得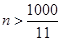 ,故满足
,故满足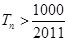 的最小正整数为91.
的最小正整数为91.
【解析】略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
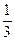 )是函数
)是函数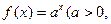 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列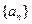 的前
的前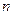 项和为
项和为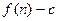 ,数列
,数列
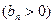 的首项为
的首项为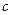 ,且前
,且前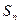 满足
满足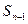 =
=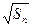 +
+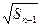 (
(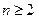 ).
).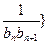 前
前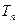 ,问
,问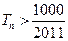 的最小正整数
的最小正整数
 为常数,且
为常数,且 ,函数
,函数 ,
, (
( ,为自然对数的底数)
,为自然对数的底数) 的值;
的值; 的单调区间;
的单调区间; 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( ,直线
,直线 与曲线
与曲线 (
( )都有公共点?若存在,求出最小的实数
)都有公共点?若存在,求出最小的实数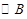
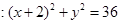 . P为
. P为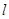 与轨迹C交于S、T两点,且
与轨迹C交于S、T两点,且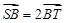 ,求直线
,求直线