题目内容

已知函数f（x）=
1
sin2x
+
2
cos2x
，则函数f（x）的最小值为
 
．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：根据同角的三角函数关系式以及1的代换，结合基本不等式的性质即可得到结论．
解答： 解：f（x）=
1
sin2x
+
2
cos2x
=
sin2x+cos2x
sin2x
+
2sin2x+2cos2x
cos2x
=1+
cos2x
sin2x
+2+
2sin2x
cos2x

≥3+2
cos2x
sin2x
•
2sin2x
cos2x
=3+2
2
，
当且仅当
cos2x
sin2x
=
2sin2x
cos2x
，
即cos4x=2sin4x，即cos2x=
2
sin2x时取等号，
故函数f（x）的最小值为3+2
2
，
故答案为：3+2
2
．
点评：本题主要考查函数最值的求解，根据三角函数1的代换，结合基本不等式成立的条件是解决本题的关键．
练习册系列答案
相关题目
已知等腰Rt△ABC中，D是斜边BC上的点，若AB=3，BD=
2
，则
AB
•
AD
=
 
．
已知α∈（π，2π），cosα=-
5
5
，tan2α=
 
．
如图所示，△A′B′C′是水平放置的平面图形的斜二测直观图，将其还原成平面图形．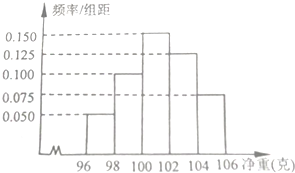
某工厂为了了解一批产品的净重（单位：克）情况，从中随机抽测了100件产品的净重，所得数据均在区间[96，106]中，其频率分布直方图如图所示，则在抽测的100件产品中，净重在区间[100，104]上的产品件数是
 
．
已知等差数列{an}中，a1=1，a3=3；
（1）求数列{an}的通项公式；
（2）若数列{an}的前k项和Sk=36，求k的值；
（3）证明：数列{an-1}也是等差数列．
已知函数f（x）=sinx+
3
cosx则下列命题正确的是
 
  （写出所有正确命题的编号）
①f（x）的最大值为2．；
②f（x）的图象关于点（-
π
6
，0）对称；
③f（x）在区间（-
5π
6
，
π
6
）上单调递增；
④若实数m使得方程f（x）=m在[0，2π]上恰好有三个实数解x1，x2，x3，则x1+x2+x3=
7π
3
；
⑤f（x）的图象与g（x）=sin（x-
2π
3
）的图象关于x轴对称．
求下列函数的定义域：
（1）y=
1
1-tanx
；
（2）y=
1
1+2tanx
；
（3）y=-tan（x+
π
6
）+2；
（4）y=
1-cos
x
2
．
已知f（x）=
1
x×(x+1)
，则f（1）=
1
1×(1+1)
=
1
1×2
；f（2）=
1
2×(2+1)
=
1
2×3
；…已知f（1）+f（2）+f（3）+…+f（n）=
14
15
，求n的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网