题目内容
15.设f(x)=$\frac{\sqrt{{x}^{4}-3{x}^{2}+9}-\sqrt{{x}^{4}-4{x}^{2}+9}}{x}$(x>0)(1)将f(x)化成$\frac{1}{\sqrt{{g}^{2}(x)+a}+\sqrt{{g}^{2}(x)+b}}$(a,b是不同的整数)的形式;
(2)求f(x)的最大值及相应的x值.
分析 (1)采取分子有理化,以及完全平方式即可求出,
(2)设h(x)=(x-$\frac{3}{x}$)2,x>0当x=$\frac{3}{x}$时,即x=$\sqrt{3}$时,h(x)有最小值,则f(x)有最大值,代值计算即可.
解答 解:(1)f(x)=$\frac{\sqrt{{x}^{4}-3{x}^{2}+9}-\sqrt{{x}^{4}-4{x}^{2}+9}}{x}$=$\frac{{x}^{4}-3{x}^{2}+9-{x}^{4}+4{x}^{2}-9}{{x}^{2}•\frac{1}{x}(\sqrt{{x}^{4}-3{x}^{2}+9}+\sqrt{{x}^{4}-4{x}^{2}+9})}$=$\frac{1}{\sqrt{{x}^{2}+\frac{9}{{x}^{2}}-3}+\sqrt{{x}^{2}+\frac{9}{{x}^{2}}-4}}$=$\frac{1}{\sqrt{(x-\frac{3}{x})^{2}+3}+\sqrt{(x-\frac{3}{x})^{2}+2}}$
(2)设h(x)=(x-$\frac{3}{x}$)2,x>0
当x=$\frac{3}{x}$时,即x=$\sqrt{3}$时,h(x)有最小值,则f(x)有最大值,
∴f(x)max=f($\sqrt{3}$)=$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$.
点评 本题考查了函数的化简与求值,关键是化简,属于中档题.

练习册系列答案
相关题目
5.“a>0,b>0”是“方程ax2+by2=1表示椭圆”的( )
| A. | 充要条件 | B. | 充分非必要条件 | ||
| C. | 必要非充分条件 | D. | 既不充分也不必要条件 |
10.某几何体的三视图如图所示.则其体积积为( )


| A. | 8π | B. | $\frac{17}{2}π$ | C. | 9π | D. | $\frac{15}{2}π$ |
20.在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)中,c2=a2+b2,直线x=-$\frac{{a}^{2}}{c}$与双曲线的两条渐近线交于A,B两点,且左焦点在以AB为直径的圆内,则该双曲线的离心率的取值范围( )
| A. | (0,$\sqrt{2}$) | B. | (1,$\sqrt{2}$) | C. | ($\frac{\sqrt{2}}{2}$,1) | D. | ($\sqrt{2}$,+∞) |
7. 如图,网格纸上正方形小格的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )
 如图,网格纸上正方形小格的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | 25 | B. | 27 | C. | 30 | D. | 35 |
4.已知x,y满足不等式$\left\{\begin{array}{l}{x≥0}\\{x-y+2≤0}\\{2x+y-5≤0}\end{array}\right.$,则z=(x-1)2+y2的最小值为( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 5 |
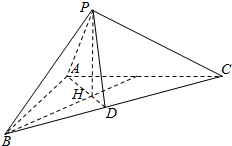 如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.
如图,三棱锥P-ABC中,AB=6,AC=8,D是BC的中点,AD=$\frac{1}{2}$BC,P在平面ABC上的射影H是△ABC的重心,PH=4.