Question

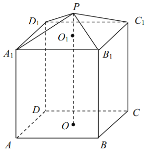
【题目】现需要设计一个仓库，由上下两部分组成，上部的形状是正四棱锥，下部的形状是正四棱柱（如图所示），并要求正四棱柱的高是正四棱锥的高的4倍.

（1）若，，则仓库的容积是多少？

（2）若正四棱锥的侧棱长为，当为多少时，下部的正四棱柱侧面积最大，最大面积是多少？

Answer 1

【答案】（1）（2）当为时，下部分正四棱柱侧面积最大，最大面积是.

【解析】

（1）直接利用棱锥和棱柱的体积公式求解即可；

（2）设，下部分的侧面积为，由已知正四棱柱的高是正四棱锥的高的4倍.可以求出的长，利用正四棱锥的侧棱长，结合勾股定理，可以求出的长，由正方形的性质，可以求出的长，这样可以求出的表达式，利用配方法，可以求出的最大值.

（1），则，

.

，

故仓库的容积为.

（2）设，下部分的侧面积为，

则，

，，

，

设，

当即时，，

答：当为时，下部分正四棱柱侧面积最大，最大面积是.