题目内容
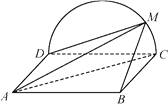
【题目】平面四边形![]() 中,
中,![]() .
.
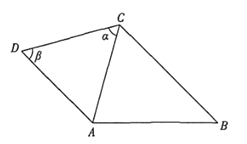
(1)若![]() ,求
,求![]() ;
;
(2)设![]() ,若
,若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 法一:在![]() 中,利用余弦定理即可得到
中,利用余弦定理即可得到![]() 的长度;
的长度;
法二:在![]() 中,由正弦定理可求得
中,由正弦定理可求得![]() ,再利用正弦定理即可得到
,再利用正弦定理即可得到![]() 的长度;
的长度;
(2)在![]() 中,使用正弦定理可知
中,使用正弦定理可知![]() 是等边三角形或直角三角形,分两种情况分别找出面积表达式计算最大值即可.
是等边三角形或直角三角形,分两种情况分别找出面积表达式计算最大值即可.
(1)法一:![]() 中,由余弦定理得
中,由余弦定理得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() 舍去,
舍去,
所以![]() .
.
法二:![]() 中,由正弦定理得
中,由正弦定理得![]() ,即
,即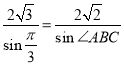 .
.
解得![]() ,故
,故![]() ,
,
![]() .
.
由正弦定理得![]() ,即
,即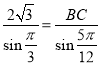 ,解得
,解得![]() .
.
(2)![]() 中,由正弦定理及
中,由正弦定理及![]() ,可得
,可得![]() ,即
,即![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
![]() 是等边三角形或直角三角形.
是等边三角形或直角三角形.
![]() 中,设
中,设![]() ,由正弦定理得
,由正弦定理得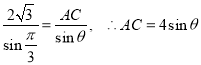 .
.
若![]() 是等边三角形,则
是等边三角形,则
![]() .
.
∵![]() 当
当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;
;
若![]() 是直角三角形,则
是直角三角形,则![]() .
.
![]() 当
当![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ;
;
综上所述,![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
相关题目