数列1,1+2,1+2+4,-,1+2+22+-+2n-1,-的前n项和Sn>1020,那么n的最小值是( ) (A)7 (B)8 (C)9 (D)10 题目和参考答案——青夏教育精英家教网——

题目内容

数列1,1+2,1+2+4,…,1+2+2²+…+2^n-1,…的前n项和S_n>1020,那么n的最小值是(　　)

(A)7 (B)8 (C)9 (D)10

D解析:a_n=1+2+2²+…+2^n-1=2ⁿ-1.

∴S_n=(2¹-1)+(2²-1)+…+(2ⁿ-1)

=(2¹+2²+…+2ⁿ)-n

=2ⁿ⁺¹-n-2.

∴S₉=1013<1020,S₁₀=2036>1020.

∴S_n>1020,n的最小值是10.

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

已知数列是等差数列，若，且_，则_______．

若等差数列{a_n}满足a₇+a₈+a₉>0,a₇+a₁₀<0,则当n=　　　　时,{a_n}的前n项和最大.

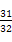等比数列{a_n}的首项a₁=-1,前n项和为S_n,若=,则{a_n}的通项公式a_n=　　　　.

.数列{1+2^n-1}的前n项和为(　　)

(A)1+2ⁿ (B)2+2ⁿ

(C)n+2ⁿ-1 (D)n+2+2ⁿ

设{a_n}是公差大于零的等差数列,已知a₁=2,a₃=-10.

(1)求{a_n}的通项公式;

(2)设{b_n}是以函数y=4sin²πx的最小正周期为首项,以3为公比的等比数列,求数列{a_n-b_n}的前n项和S_n.

已知数列的通项公式为，则(　　)

A．不是数列中的项 B．只是数列中的第2项

C．只是数列中的第6项 D．是数列中的第2项或第6项

已知数列满足，则=( )

A．0 B． C． D．

已知数列{a_n}满足a_n₊₂=－a_n（n∈N^*），且a₁=1，a₂=2，则该数列前2005项的和为( )

A.0 B.－3 C.3 D.1