题目内容
在直角坐标系上xOy中，角α的顶点为坐标原点，始边在x轴的正半轴上，当角α的终边在直线l：y=3x上时．
求：（1）
的值；
（2）
的值．
求：（1）
| sinα+cosα |
| sinα-cosα |
（2）
| sinαcosα |
| sin2α+2 |
考点：任意角的三角函数的定义,三角函数的化简求值
专题：三角函数的求值
分析：由角α的终边在直线l：y=3x上分类求出tanα的值，然后把（1）（2）中的正弦和余弦化为正切求解．
解答：
解：当角α的终边在直线l：y=3x上且位于第一象限时，tanα=3；当角α的终边在直线l：y=3x上且位于第三象限时，tanα=-3．
若tanα=3．
（1）
=
=
=2．
（2）
=
=
=
=
；
若tanα=-3．
（1）
=
=
=
．
（2）
=
=
=
=-
．
若tanα=3．
（1）
| sinα+cosα |
| sinα-cosα |
| tanα+1 |
| tanα-1 |
| 3+1 |
| 3-1 |
（2）
| sinαcosα |
| sin2α+2 |
| sinαcosα |
| 3sin2α+2cos2α |
| tanα |
| 3tan2α+2 |
| 3 |
| 3×32+2 |
| 3 |
| 29 |
若tanα=-3．
（1）
| sinα+cosα |
| sinα-cosα |
| tanα+1 |
| tanα-1 |
| -3+1 |
| -3-1 |
| 1 |
| 2 |
（2）
| sinαcosα |
| sin2α+2 |
| sinαcosα |
| 3sin2α+2cos2α |
| tanα |
| 3tan2α+2 |
| -3 |
| 3×(-3)2+2 |
| 3 |
| 29 |
点评：本题考查了三角函数的化简与求值，关键是注意“齐次式”的应用，是中档题．
练习册系列答案
相关题目
下列函数中，定义域和值域相同的是（ ）
| A、y=x2和y=2x |
| B、y=sinx和y=tanx |
| C、y=x3和y=log2x |
| D、y=x2和y=|x| |
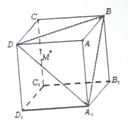如图，在棱长为1的正方体ABCD-A1B1C1D1中，设M是△A1BD内任一点（不包括边界），定义f（M）=（m，n，p），其中m，n，p分别是点M到平面ADD1A1，平面ABB1A1，平面ABCD的距离，若f（M）=（