题目内容
19.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且(3+b)(sinA-sinB)=(c-b)sinC,且a=3,则△ABC面积的最大值为$\frac{{9\sqrt{3}}}{4}$.分析 由(3+b)(sinA-sinB)=(c-b)sinC,a=3,利用正弦定理可得(a+b)(a-b)=(c-b)c,化简利用余弦定理可得A,再利用余弦定理、基本不等式的性质、三角形面积计算公式即可得出.
解答 解:∵(3+b)(sinA-sinB)=(c-b)sinC,a=3,
∴(a+b)(a-b)=(c-b)c,
∴b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),∴A=$\frac{π}{3}$.
∴b2+c2=9+bc≥2bc,化为bc≤9,当且仅当b=c=3时取等号.
∴S△ABC=$\frac{1}{2}bcsinA$$≤\frac{1}{2}×9×sin\frac{π}{3}$=$\frac{9\sqrt{3}}{4}$.
故最大值为:$\frac{{9\sqrt{3}}}{4}$.
点评 本题考查了正弦定理余弦定理、基本不等式的性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知{an}是各项均为正项的等比数列,且3a1,$\frac{1}{2}{a_3}$,2a2成等差数列,则$\frac{{{a_{2014}}+{a_{2015}}}}{{{a_{2012}}+{a_{2013}}}}$=( )
| A. | 3或-1 | B. | 9或1 | C. | 1 | D. | 9 |
14.下列函数既是偶函数,又在(0,π)上单调递增的是( )
| A. | y=|sinx| | B. | y=tan|x| | C. | y=cosx | D. | y=-cosx |
11.若z•(1+i)=2-i(i为虚数单位),则复数z的虚数部分为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$i | D. | -$\frac{3}{2}$i |
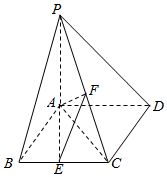 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.