题目内容
已知椭圆 ,P为椭圆上除长轴端点外的任一点,F1,F2为椭圆的两个焦点.
,P为椭圆上除长轴端点外的任一点,F1,F2为椭圆的两个焦点.(1)若∠PF1F2=α,∠PF1F2=β,求证:离心率
 ;
;(2)若∠F1PF2=2θ,求证:△F1PF2的面积为b2•tanθ.
【答案】分析:(1)根据∵∠PF1F2和∠PF1F2求得∠F1PF2,进而根据正弦定理分别求得|PF1|和|PF2|,代入|PF1|+|PF2|=2a中求得a和c的关系,求得离心率.
(2)设PF1=x,PF2=y,根据椭圆的定义可知x+y=2a,进而可得x2+y2=4a2-2xy代入余弦定理中,求得xy,然后根据三角形面积公式化简整理即可得出答案.
解答:(1)证明∵∠PF1F2=α,∠PF1F2=β,
∴∠F1PF2=180°-α-β
∴sin∠F1PF2=sin(α+β)
由正弦定理可得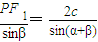 ,
,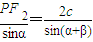
∴|PF1|=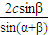 ,|PF2|=
,|PF2|=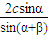
根据椭圆的定义可知|PF1|+|PF2|=2a
∴a=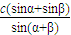 =c•
=c•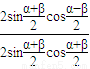 =c•
=c•
∴e=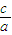 =
=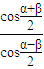
(2)证明:设PF1=x,PF2=y
则根据椭圆的定义可知x+y=2a,
∴x2+y2=4a2-2xy
由余弦定理可知cos2θ=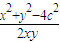 =
=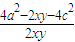
∴xy=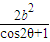 =
=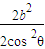
∴:△F1PF2的面积S= xysin2θ=
xysin2θ=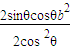 =
= =b2•tanθ
=b2•tanθ
点评:本题主要考查了椭圆的应用及解三角形问题.解题的关键是充分利用椭圆的定义,找到三角形三边的关系,进而通过正弦定理和余弦定理转化成三角函数的化简.
(2)设PF1=x,PF2=y,根据椭圆的定义可知x+y=2a,进而可得x2+y2=4a2-2xy代入余弦定理中,求得xy,然后根据三角形面积公式化简整理即可得出答案.
解答:(1)证明∵∠PF1F2=α,∠PF1F2=β,
∴∠F1PF2=180°-α-β
∴sin∠F1PF2=sin(α+β)
由正弦定理可得
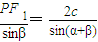 ,
,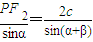
∴|PF1|=
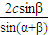 ,|PF2|=
,|PF2|=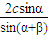
根据椭圆的定义可知|PF1|+|PF2|=2a
∴a=
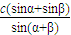 =c•
=c•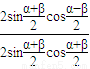 =c•
=c•
∴e=
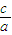 =
=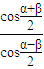
(2)证明:设PF1=x,PF2=y
则根据椭圆的定义可知x+y=2a,
∴x2+y2=4a2-2xy
由余弦定理可知cos2θ=
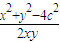 =
=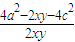
∴xy=
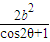 =
=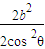
∴:△F1PF2的面积S=
 xysin2θ=
xysin2θ=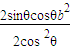 =
= =b2•tanθ
=b2•tanθ点评:本题主要考查了椭圆的应用及解三角形问题.解题的关键是充分利用椭圆的定义,找到三角形三边的关系,进而通过正弦定理和余弦定理转化成三角函数的化简.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目