题目内容
已知点P是抛物线y=2x2+1上的动点，定点A（0，-1），若点M分
所成的比为2，则点M的轨迹方程是 ，它的焦点坐标是 ．
【答案】分析：设P（x，y），M（x，y），由定比分点坐标公式得到点M与点P坐标间的关系式，由此关系式代入点P所满足的方程y=2x2+1，消去x和y0，转化为x、y的方程．
解答：解析设P（x，y），M（x，y），
⇒
，
代入y=2x2+1得3y+2=18x2+1，
即18x2=3y+1，x2=
y+
=
（y+
），
∴p=
，焦点坐标为（0，-
）．
答案：x2=
（y+
）（0，-
）
点评：用代入法求轨迹方程，联系曲线写出焦点坐标．
解答：解析设P（x，y），M（x，y），
⇒，代入y=2x2+1得3y+2=18x2+1，
即18x2=3y+1，x2=
y+=（y+），∴p=
，焦点坐标为（0，-）．答案：x2=
（y+）（0，-）点评：用代入法求轨迹方程，联系曲线写出焦点坐标．
练习册系列答案
相关题目
所成的比为2,则点M的轨迹方程是_____________,它的焦点坐标是_________________.
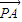所成的比为2，则点M的轨迹方程是 ，它的焦点坐标是 ．