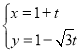题目内容
【题目】已知![]() 函数
函数![]()
(1)当![]() 时,解不等式
时,解不等式![]()
(2)若关于![]() 的方程
的方程![]() 的解集中怡好有一个元素,求
的解集中怡好有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() 若对任意
若对任意![]() 函数
函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)当![]() 时,解对数不等式即可.
时,解对数不等式即可.
(2)根据对数的运算法则进行化简,转化为一元二次方程,讨论![]() 的取值范围进行求解即可.
的取值范围进行求解即可.
(3)根据条件得到![]() 恒成立,利用换元法进行转化,结合对勾函数的单调性进行求解即可.
恒成立,利用换元法进行转化,结合对勾函数的单调性进行求解即可.
解:(1)当![]() 时,
时,![]() ,
,
由![]() ,得
,得![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
即不等式的解集为![]() 或
或![]() ;
;
(2)由![]() 得
得![]() .
.
即![]() ,
,
即![]() ,①
,①
则![]() ,
,
即![]() ,②,
,②,
当![]() 时,方程②的解为
时,方程②的解为![]() ,代入①,成立
,代入①,成立
当![]() 时,方程②的解为
时,方程②的解为![]() ,代入①,成立
,代入①,成立
当![]() 且
且![]() 时,方程②的解为
时,方程②的解为![]() 或
或![]() ,
,
若![]() 是方程①的解,则
是方程①的解,则![]() ,即
,即![]() ,
,
若![]() 是方程①的解,则
是方程①的解,则![]() ,即
,即![]() ,
,
则要使方程①有且仅有一个解,则![]() .
.
综上,若方程![]() 的解集中恰好有一个元素,
的解集中恰好有一个元素,
则![]() 的取值范围是
的取值范围是![]() 或
或![]() 或
或![]() .
.
(3)函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
由题意得![]() ,
,
即![]() ,
,
即![]() 即
即![]()
设![]() ,则
,则![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,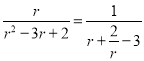 ,
,
![]() 在
在![]() 上递减,
上递减,
![]() ,
,
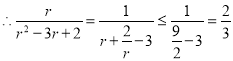 ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目