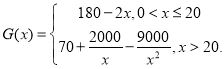题目内容
【题目】已知函数
.
（1）若函数
在区间
上存在零点，求实数
的取值范围；
（2）若对任意的
，总存在
使得
成立，求实数的取值范围.
【答案】（1）
；（2）
.
【解析】
（1）根据
对称轴
分析零点存在时对应的
的范围；
（2）根据条件分析可得：
的值域应为
的值域的子集，此时注意对与
的关系进行分类讨论，由此得到满足条件的的取值范围.
（1）因函数
的对称轴是
，
所以
在区间
上是减函数，
因函数在区间上存在零点，则必有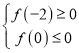
，
即
解得
.
故所求实数的取值范围
.
（2）若对任意的
，总存在
使得
成立，只需函数的值域为函数
的值域的子集.
在区间
的值域为
,
①当
时，
为常数，不符合题意舍去；
②当
时，
在区间
的值域为
，
所以
，解得
.
③当
时，在区间的值域为
，
所以
，无解.
综上所述实数的取值范围
.
练习册系列答案
相关题目
【题目】南充高中扎实推进阳光体育运动，积极引导学生走向操场，走进大自然，参加体育锻炼，每天上午第三节课后全校大课间活动时长35分钟．现为了了解学生的体育锻炼时间，采用简单随机抽样法抽取了100名学生，对其平均每日参加体育锻炼的时间（单位：分钟）进行调查，按平均每日体育锻炼时间分组统计如下表：
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
（1）将频率视为概率，估计我校7000名学生中“锻炼达人”有多少?
（2）从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人；
②若从这5人中随机抽取2人作为组长候选人，求抽取的2人中男生和女生各1人的概率.
