题目内容
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若不等式
,若不等式![]() 对
对![]() 都成立,求实数
都成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 且
且![]() 时,求函数
时,求函数![]() 的零点.
的零点.
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() (3)见解析
(3)见解析
【解析】
(1)根据根与系数关系列方程组,解方程组求得![]() 的值.
的值.
(2)将不等式![]() 转化为
转化为![]() ,求得左边函数
,求得左边函数![]() 的最小值,由此解一元二次不等式求得
的最小值,由此解一元二次不等式求得![]() 的取值范围.
的取值范围.
(3)利用判别式进行分类讨论,结合函数![]() 的定义域,求得函数
的定义域,求得函数![]() 的零点.
的零点.
(1)因为不等式![]() 的解集为
的解集为![]() ,所以-3,1为方程
,所以-3,1为方程![]() 的两个根,
的两个根,
由根与系数的关系得
![]() ,即
,即![]() ,
,![]() .
.
(2)当![]() 时,
时,![]() ,
,
因为不等式![]() 对
对![]() 都成立,
都成立,
所以不等式![]() 对任意实数
对任意实数![]() 都成立.
都成立.
令![]() ,
,
所以![]() .
.
当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() ,得
,得![]() 或
或![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)当![]() 时,
时,![]() ,
,
函数![]() 的图像是开口向上且对称轴为
的图像是开口向上且对称轴为![]() 的抛物线,
的抛物线,
![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 无零点.
无零点.
②当![]() ,即
,即![]() 或
或![]() 时,
时,
(ⅰ)当![]() 时,
时,![]() ,此时函数
,此时函数![]() 无零点.
无零点.
(ⅱ)当![]() 时,
时,![]() ,此时函数
,此时函数![]() 有零点3.
有零点3.
③当![]() ,即
,即![]() 或
或![]() 时,令
时,令![]() ,得
,得
![]() ,
,![]()
![]() .
.
(ⅰ)当![]() 时,得
时,得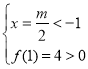 ,此时
,此时![]() ,
,
所以当![]() 时,函数
时,函数![]() 无零点.
无零点.
(ⅱ)当![]() 时,得
时,得 ,此时
,此时![]() ,所以当
,所以当![]() 时,函数
时,函数![]() 有两个零点:
有两个零点:![]() ,
,![]() .
.
综上所述:当![]() ,
,![]() 时,函数
时,函数![]() 无零点;
无零点;
当![]() ,
,![]() 时,函数
时,函数![]() 有一个零点为3;
有一个零点为3;
当![]() ,
,![]() 时,函数
时,函数![]() 有两个零点:
有两个零点:![]() ,
,![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目