题目内容
2.若f′(x)是f(x)=$\frac{1}{3}$x3-2x+1的导函数,则f′(2)=2.分析 先求函数f(x)的导函数,然后在导函数解析式中把x代2求值.
解答 解:因为函数f(x)=$\frac{1}{3}$x3-2x+1,
所以其导函数 f′(x)=x2-2,
所以f′(2)=22-2=2,
故答案为:2.
点评 本题考查了导数的运算,已知函数解析式,求函数在x取某一具体值时的导数值属于基础题.

练习册系列答案
相关题目
12.等差数列{an}前n项和为Sn,${S_p}=\frac{p}{q}$,${S_q}=\frac{q}{p}$(p≠q),则Sp+q的值是( )
| A. | 大于4 | B. | 小于4 | C. | 等于4 | D. | 不确定 |
7.在△OAB中,已知OA=5,OB=4,点P是AB的中点,则$\overrightarrow{OP}•\overrightarrow{AB}$=( )
| A. | 10 | B. | -$\frac{9}{2}$ | C. | 20 | D. | -20 |
11.曲线$\left\{\begin{array}{l}x=5cosθ\\ y=4sinθ\end{array}$(θ为参数)的焦点到双曲线x2-$\frac{y^2}{2}$=1的渐近线的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{10}$ |
12.下列四个函数中,在定义域上是减函数的是( )
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x3 | C. | f(x)=-x2 | D. | f(x)=-x |
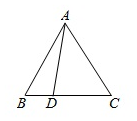 如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.
如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.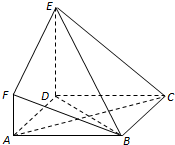 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3$\sqrt{6}$.