题目内容
设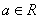 ,函数
,函数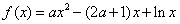 .
.
(I)当 时,求
时,求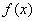 的极值;[
的极值;[
(II)设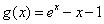 ,若对于任意的
,若对于任意的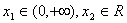 ,不等式
,不等式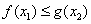 恒成立,求实数
恒成立,求实数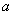 的取值范围.
的取值范围.
(Ⅰ)当 时,函数
时,函数 ,则
,则 .
.
 得:
得:
当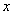 变化时,
变化时, ,
,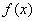 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大 |
| 极小 |
|
因此,当 时,
时,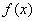 有极大值,并且
有极大值,并且 ;
;
当 时,
时,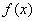 有极小值,并且
有极小值,并且 .
.
(Ⅱ)由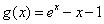 ,则
,则 ,
,
解 得
得 ;解
;解 得
得
所有 在
在 是减函数,在
是减函数,在 是增函数,
是增函数,
即
对于任意的 ,不等式
,不等式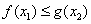 恒成立,则有
恒成立,则有 即可.
即可.
即不等式 对于任意的
对于任意的 恒成立
恒成立

(1)当 时,
时, ,解
,解 得
得 ;解
;解 得
得
所以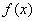 在
在 是增函数,在
是增函数,在 是减函数,
是减函数, ,
,
所以 符合题意.
符合题意.
(2)当 时,
时, ,解
,解 得
得 ;解
;解 得
得
所以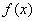 在
在 是增函数,在
是增函数,在 是减
是减 函数,
函数, ,
,
得 ,所以
,所以 符合题意.
符合题意.
(3)当 时,
时, ,
, 得
得
 时,
时, ,
,
解 得
得 或
或 ;解
;解 得
得
所以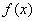 在
在 是增函数,
是增函数,
而当 时,
时, ,这与对于任意的
,这与对于任意的 时
时 矛盾
矛盾
同理 时也不成立.
时也不成立.
综上所述,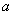 的取值范围为
的取值范围为 .-
.-

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是
A.30.5 B.31.5 C.31 D.32
| 1 | 0 | 2 | ||
| 2 | 0 | 1 | 4 | |
| 3 | 1 | 1 | 2 | 6 |
| 4 | 3 | 8 |








 ,
, (
( 为虚数单位).在复平面内,
为虚数单位).在复平面内, 对应的点在第 象限.
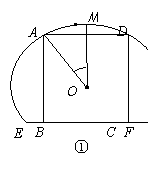
对应的点在第 象限.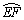 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=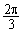 .将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在
.将弓形薄铁片裁剪成尽可能大的矩形铁片ABCD(不计损耗), AD∥EF,且点A、D在 .
.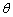 的函数关系式;
的函数关系式;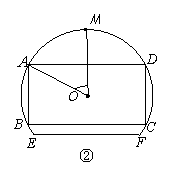 (2)当矩形铁片ABCD的
(2)当矩形铁片ABCD的 面积最大时,求cos
面积最大时,求cos
 的一个单调
的一个单调 B.
B.  C.
C.  D.
D. 
 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,已知角
,已知角 为锐角,且
为锐角,且  ,则实数
,则实数 范围为
范围为
 ,则
,则 ( )
( ) B.[1,2] C.
B.[1,2] C.  D.
D. 
 :
: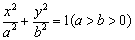 的离心率为
的离心率为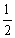 ,右焦点为
,右焦点为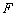 ,右顶点
,右顶点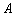 在
在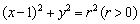 上.
上. 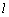 与椭圆
与椭圆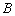 ,与圆
,与圆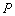 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线 的中点,若存在,求出直线
的中点,若存在,求出直线