题目内容
已知椭圆 :
: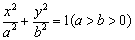 的离心率为
的离心率为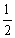 ,右焦点为
,右焦点为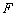 ,右顶点
,右顶点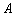 在
在
圆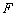 :
: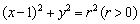 上.
上.
(Ⅰ)求椭圆 和圆
和圆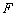 的方程;
的方程;
(Ⅱ)已知过点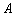 的直线
的直线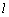 与椭圆
与椭圆 交于另一点
交于另一点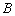 ,与圆
,与圆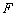 交于另一点
交于另一点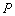 .请判断是否存在斜率不为0的直线
.请判断是否存在斜率不为0的直线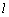 ,使点
,使点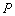 恰好为线段
恰好为线段 的中点,若存在,求出直线
的中点,若存在,求出直线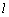 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解:(Ⅰ)由题意可得 , -
, -
又由题意可得 ,
,
所以 , -
, -
所以 ,
,
所以椭圆 的方程为
的方程为 .
.
所以椭圆 的右顶点
的右顶点 , 代入圆
, 代入圆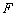 的方程,可得
的方程,可得 ,
,
所以圆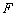 的方程为
的方程为 .
.
(Ⅱ)法1:
假设存在直线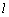 :
:
 满足条件,
满足条件,
由 得
得 -
-
设 ,则
,则 ,
,
可得中点 , -
, -
由点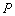 在圆
在圆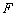 上可得
上可得
化简整理得
又因为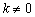 ,
,
所以不存在满足条件的直线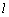 .
.
(Ⅱ)法2:
假设存在直线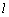 满足题意.
满足题意.
由(Ⅰ)可得 是圆
是圆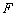 的直径,
的直径,
所以 . -
. -
由点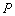 是
是 中点,可得
中点,可得 .
.
设点 ,则由题意可得
,则由题意可得 .
.
又因为直线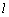 的斜率不为0,所以
的斜率不为0,所以 , -
, -
所以 ,-
,-
这与 矛盾,所以不存在满足条件的直线
矛盾,所以不存在满足条件的直线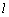 .
.

 期末集结号系列答案
期末集结号系列答案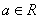 ,函数
,函数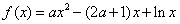 .
. 时,求
时,求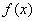 的极值;[
的极值;[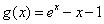 ,若对于任意的
,若对于任意的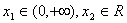 ,不等式
,不等式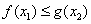 恒成立,求实数
恒成立,求实数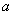 的取值范围.
的取值范围. ,能使方程
,能使方程 两根均为实数的概率为 .
两根均为实数的概率为 . 中,若
中,若 ,面积记作
,面积记作 ,则下列结论中一定成立的是
,则下列结论中一定成立的是 B.
B. C.
C. D.
D.
 与抛物线
与抛物线 交于
交于 两点,点
两点,点 ,其中
,其中 为抛物线
为抛物线 与
与 平行时,
平行时, ________;
________; ,
, 不是等边三角形;
不是等边三角形;
 且
且 ,使得
,使得 与
与 垂直;
垂直; 总成立.
总成立. 的值为6,那么运行相应程序,输出的
的值为6,那么运行相应程序,输出的 的值为
的值为 A. 3 B. 5
A. 3 B. 5  :
: (
( 为参数)的圆心坐标为__________;直线
为参数)的圆心坐标为__________;直线 :
: 被圆
被圆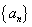 为等差数列,若
为等差数列,若 ,
, ,则公差
,则公差 .
. 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间. 的值及参加“掷实心球”项目
的值及参加“掷实心球”项目 