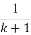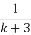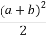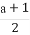Question

已知函数f(x)=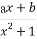在点(-1,f(-1))处的切线方程为x+y+3=0.

(1)求函数f(x)的解析式.

(2)设g(x)=lnx.求证:g(x)≥f(x)在[1,+∞)上恒成立.

 

Answer 1

(1) f(x)=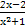 (2)见解析

【解析】(1)将x=-1代入切线方程得y=-2.

∴f(-1)=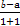=-2,化简得b-a=-4.

又f'(x)=,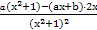

∴f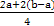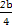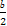'(-1)====-1,

则可得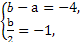

解得a=2,b=-2,

∴f(x)=.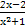

(2)由已知得lnx≥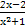在[1,+∞)上恒成立,

化简得(x2+1)lnx≥2x-2,

即x2lnx+lnx-2x+2≥0在[1,+∞)上恒成立.

设h(x)=x2lnx+lnx-2x+2,

则h'(x)=2xlnx+x+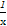-2,

∵x≥1,∴2xlnx≥0,

x+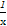≥2,即h'(x)≥0,

∴h(x)在[1,+∞)上单调递增,

∴h(x)≥h(1)=0,

∴g(x)≥f(x)在[1,+∞)上恒成立.