题目内容
解关于 的不等式
的不等式 .
.
当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,不等式的解集为
时,不等式的解集为 。
。
解析试题分析:解关于 的含参不等式,分三方面讨论①二次项系数②判别式的符号③两根的大小
的含参不等式,分三方面讨论①二次项系数②判别式的符号③两根的大小
本题中二次项系数 ,
, ,方程的两根
,方程的两根
故只需对两根的大小进行讨论,即可结合二次函数的图像写出不等式的解集
试题解析:不等式 即
即 .
.
∵ ,不等式可以化为
,不等式可以化为 .
.
若 ,则
,则 ,此时不等式的解集为
,此时不等式的解集为 ;
;
若 ,则不等式为
,则不等式为 ,不等式的解集为
,不等式的解集为 ;
;
若 ,则
,则 ,此时不等式的解集为
,此时不等式的解集为 .
.
综上所述,
当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,不等式的解集为
时,不等式的解集为 。
。
考点:解含参不等式

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +
+ ≥m恒成立的实数m的取值范围为 .
≥m恒成立的实数m的取值范围为 . 的最大值为 .
的最大值为 . ,观察下列不等式:
,观察下列不等式: ,
, ,…,请你猜测
,…,请你猜测 将满足的不等式,并用数学归纳法加以证明。
将满足的不等式,并用数学归纳法加以证明。
 ;
;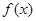 的最小值.
的最小值. (2)
(2)
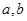 满足
满足 ,证明:
,证明: .
.