题目内容
若 ,观察下列不等式:
,观察下列不等式: ,
, ,…,请你猜测
,…,请你猜测 将满足的不等式,并用数学归纳法加以证明。
将满足的不等式,并用数学归纳法加以证明。
(x1+x2+…+xn)( )≥n2(n≥2),证明见解析
)≥n2(n≥2),证明见解析
解析试题分析:根据不等式:(x1+x2)( )≥4,(x1+x2+x3)(
)≥4,(x1+x2+x3)( )≥9,…,可以猜测(x1+x2+…+xn)(
)≥9,…,可以猜测(x1+x2+…+xn)( )≥n2(n≥2),再用数学归纳法证明.
)≥n2(n≥2),再用数学归纳法证明.
试题解析:将满足的不等式为 ,
,
证明如下: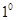 当
当 时,结论成立;
时,结论成立;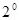 假设
假设 时,结论成立,即
时,结论成立,即
那么,当 时,
时,




显然,当 时,结论成立。
时,结论成立。
由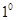 ,
,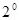 知对于大于
知对于大于 的整数
的整数 ,
, 成立。(12分)
成立。(12分)
考点:用数学归纳法证明不等式.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目

 ;
; 的解集为空集,求实数
的解集为空集,求实数 的取值范围.
的取值范围. 的不等式
的不等式 .
.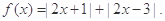
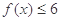 的解集;
的解集;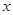 的不等式
的不等式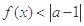 的解集非空,求实数
的解集非空,求实数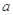 的取值范围.
的取值范围. .
. ;
; ,
,  都成立,求实数
都成立,求实数 的取值范围.
的取值范围. <1,
<1, <1,求证:
<1,求证: +
+ ≥
≥ .
. 的大小关系为 .
的大小关系为 .