题目内容
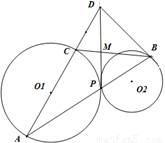
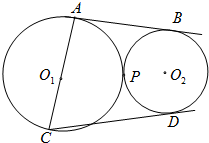 如图,已知圆O1与圆O2外切于点P,直线AB是两圆的外公切线,分别与两圆相切于A、B两点,AC是圆O1的直径,过C作圆O2的切线,切点为D.
如图,已知圆O1与圆O2外切于点P,直线AB是两圆的外公切线,分别与两圆相切于A、B两点,AC是圆O1的直径,过C作圆O2的切线,切点为D.(Ⅰ)求证:C,P,B三点共线;
(Ⅱ)求证:CD=CA.
分析:(I)连接PC,PA,PB,由于AC是圆O1的直径,可得∠APC=90°.作⊙O1与⊙O2的内公切线MP交AB与点M.利用切线的性质可得:∠BAP=∠MPA,∠MPB=∠MBP,再利用三角形的内角和定理可得∠MPA+∠MPB=∠APB=90°,进而证明上的共线.
(II)由切线的性质可得∠CAB=90°,利用射影定理可得CA2=CP•CB.再利用切割线定理可得CD2=CP•CB,即可证明.
(II)由切线的性质可得∠CAB=90°,利用射影定理可得CA2=CP•CB.再利用切割线定理可得CD2=CP•CB,即可证明.
解答:解:(Ⅰ)连接PC,PA,PB,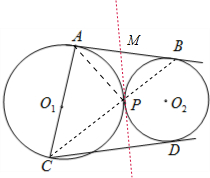
∵AC是圆O1的直径,∴∠APC=90°,
作⊙O1与⊙O2的内公切线MP交AB与点M.
又∵AB是两圆的外公切线,A,B为切点,
∴∠BAP=∠MPA,∠MPB=∠MBP,
∵∠BAP+∠APB+∠ABP=180°,
∴∠MPA+∠MPB=∠APB=90°,
∴∠CPB=180°.
∴C,P,B三点共线.
(Ⅱ)∵CD切圆O2于点D,∴CD2=CP•CB.
在△ABC中,∠CAB=90°,又∵AP⊥BC,∴CA2=CP•CB.
故CD=CA.

∵AC是圆O1的直径,∴∠APC=90°,
作⊙O1与⊙O2的内公切线MP交AB与点M.
又∵AB是两圆的外公切线,A,B为切点,
∴∠BAP=∠MPA,∠MPB=∠MBP,
∵∠BAP+∠APB+∠ABP=180°,
∴∠MPA+∠MPB=∠APB=90°,
∴∠CPB=180°.
∴C,P,B三点共线.
(Ⅱ)∵CD切圆O2于点D,∴CD2=CP•CB.
在△ABC中,∠CAB=90°,又∵AP⊥BC,∴CA2=CP•CB.
故CD=CA.
点评:本题综合考查了外切两圆的公切线的性质、射影定理和切割线定理,考查了推理能力和夹角问题的能力,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
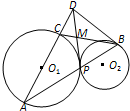 如图,已知圆O1与圆O2外切于点P,过点P的直线交圆O1于点A,交圆O2于点B,AC为O1的直径,BD切O2于B,交AC延长线于D.
如图,已知圆O1与圆O2外切于点P,过点P的直线交圆O1于点A,交圆O2于点B,AC为O1的直径,BD切O2于B,交AC延长线于D. (2012•许昌二模)如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上,
(2012•许昌二模)如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上,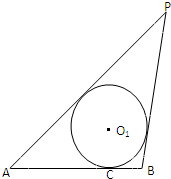 如图:已知线段AB=4,动圆O1与线段AB相切于点C,且AC-BC=2
如图:已知线段AB=4,动圆O1与线段AB相切于点C,且AC-BC=2