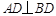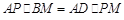题目内容
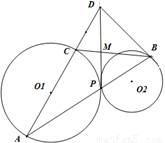
如图，已知圆O1与圆O2外切于点P，过点P的直线交圆O1于点A，交圆O2于点B，AC为O1的直径，BD切O2于B，交AC延长线于D．（1）求证：AD⊥BD；
（2）求证：若BC、PD相交于点M，则AP•BM=AD•PM．
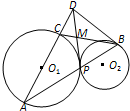
分析：（I）如图，过点P作两圆公切线交BD于T，连接PC，利用AC为直径，可得∠APC=90°，于是∠BPC=∠TPC+∠TPB=90°，又BD与⊙O2相切于B，PT为两圆公切线，可得∠TPC=∠A，∠TBP=∠TPB，得到∠A+∠TBP=90°，再利用三角形的内角和定理可得∠ADB=90°，即可证明AD⊥BD．
（II）如图所示，由（Ⅰ）易证△APC∽△ADB，利用三角形相似的性质可得对应边成比例，又由（Ⅰ）知∠ACP=∠DBP，可得P、B、D、C四点共圆，又易证△PCM∽△BDM，再利用三角形相似的性质即可得出．
（II）如图所示，由（Ⅰ）易证△APC∽△ADB，利用三角形相似的性质可得对应边成比例，又由（Ⅰ）知∠ACP=∠DBP，可得P、B、D、C四点共圆，又易证△PCM∽△BDM，再利用三角形相似的性质即可得出．
解答：证明：（Ⅰ）如图，过点P作两圆公切线交BD于T，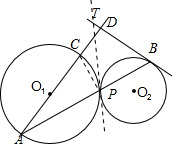
连接PC，∵AC为直径，∴∠APC=90°，
∴∠BPC=∠TPC+∠TPB=90°，
又BD与⊙O2相切于B，PT为两圆公切线，
∴∠TPC=∠A，∠TBP=∠TPB，
∴∠A+∠TBP=90°，
故∠ADB=90°，∴AD⊥BD．
（Ⅱ）如图所示，由（Ⅰ）易证△APC∽△ADB，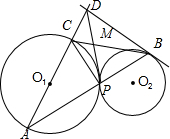
∴
=
，又由（Ⅰ）知∠ACP=∠DBP，
∴P、B、D、C四点共圆，又易证△PCM∽△BDM，∴
=
，
∴
=
，
∴AP•BM=AD•PM．
连接PC，∵AC为直径，∴∠APC=90°，
∴∠BPC=∠TPC+∠TPB=90°，
又BD与⊙O2相切于B，PT为两圆公切线，
∴∠TPC=∠A，∠TBP=∠TPB，
∴∠A+∠TBP=90°，
故∠ADB=90°，∴AD⊥BD．
（Ⅱ）如图所示，由（Ⅰ）易证△APC∽△ADB，
∴
| PC |
| BD |
| AP |
| AD |
∴P、B、D、C四点共圆，又易证△PCM∽△BDM，∴
| PC |
| BD |
| PM |
| BM |
∴
| PM |
| BM |
| AP |
| AD |
∴AP•BM=AD•PM．
点评：本题中考查了相切两圆的切线性质、弦切角定理、圆的直径的性质、三角形相似的性质、四点共圆的性质等基础知识与基本方法，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
（2012•许昌二模）如图，已知⊙O1与⊙O2外切于点P，AB是两圆的外公切线，A，B为切点，AB与O1O2的延长线相交于点C，延长AP交⊙O2于点D，点E在AD延长线上，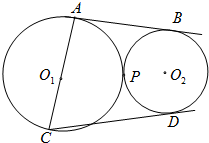
如图，已知圆O1与圆O2外切于点P，直线AB是两圆的外公切线，分别与两圆相切于A、B两点，AC是圆O1的直径，过C作圆O2的切线，切点为D．
如图：已知线段AB=4，动圆O1与线段AB相切于点C，且AC-BC=2
