题目内容
(本小题满分12分)
已知椭圆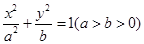 的左、右焦点分别为
的左、右焦点分别为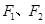 ,离心率
,离心率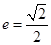 ,
, 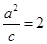 .
.
(I)求椭圆的标准方程;
(II)过点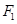 的直线
的直线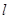 与该椭圆交于
与该椭圆交于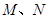 两点,且
两点,且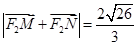 ,求直线
,求直线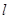 的方程.
的方程.
(I) (II)
(II)
解析试题分析:(I)由已知得 ,解得
,解得 ∴
∴ 
∴ 所求椭圆的方程为 .
.
(II)由(I)得 、
、
①若直线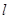 的斜率不存在,则直线
的斜率不存在,则直线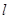 的方程为
的方程为 ,由
,由 得
得
设 、
、 ,∴
,∴  ,这与已知相矛盾。
,这与已知相矛盾。
②若直线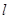 的斜率存在,设直线直线
的斜率存在,设直线直线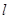 的斜率为
的斜率为 ,则直线
,则直线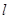 的方程为
的方程为 ,
,
设 、
、 ,联立
,联立 ,消元得
,消元得
∴  ,∴
,∴  ,
,
又∵ ∴
∴ 
∴ 
化简得 解得
解得
∴  ∴ 所求直线
∴ 所求直线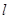 的方程为
的方程为 .
.
考点:椭圆方程及性质,直线和椭圆相交
点评:本题第二问中求直线方程要注意分斜率存在与不存在两种情况讨论

练习册系列答案
相关题目
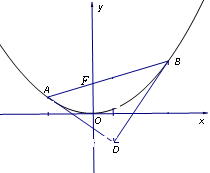
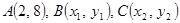 在抛物线
在抛物线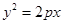 上,
上, 的重心与此抛物线的焦点F重合。
的重心与此抛物线的焦点F重合。 :
: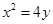 的焦点为
的焦点为 ,
, 、
、 是抛物线
是抛物线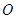 的不同两点,抛物线
的不同两点,抛物线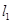 、
、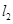 ,且
,且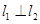 ,
, .
. 
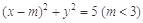 与椭圆E:
与椭圆E: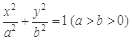 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.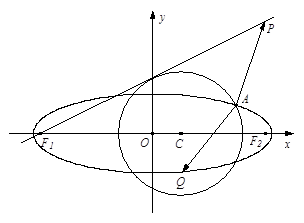
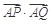 的取值范围.
的取值范围.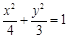 的右焦点重合,直线
的右焦点重合,直线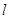 过点F交抛物线于A、B两点.
过点F交抛物线于A、B两点.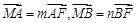 ,m、n是实数,对于直线
,m、n是实数,对于直线 、
、 两个岛屿,
两个岛屿, ,曾有渔船在距
,曾有渔船在距 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定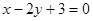 和
和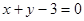 的交点,且满足下列条件的直线
的交点,且满足下列条件的直线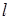 的方程.
的方程.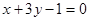 垂直;
垂直;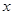 轴,
轴,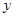 轴上的截距相等.
轴上的截距相等. :
: 的左、右焦点分别为
的左、右焦点分别为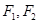 ,焦距为2,,过
,焦距为2,,过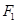 作垂直于椭圆长轴的弦长
作垂直于椭圆长轴的弦长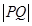 为3.
为3. 求椭圆
求椭圆 两点.并判断是否存在直线l使得
两点.并判断是否存在直线l使得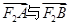 的夹角为钝角,若存在,求出l的斜率k的取值范围。
的夹角为钝角,若存在,求出l的斜率k的取值范围。 中心在原点,一个焦点为
中心在原点,一个焦点为 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是 。
。 的直线
的直线 ,使直线
,使直线 与直线
与直线