题目内容
已知抛物线 :
: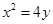 的焦点为
的焦点为 ,
, 、
、 是抛物线
是抛物线 上异于坐标原点
上异于坐标原点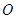 的不同两点,抛物线
的不同两点,抛物线 在点
在点 、
、 处的切线分别为
处的切线分别为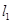 、
、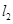 ,且
,且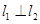 ,
,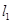 与
与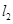 相交于点
相交于点 .
. 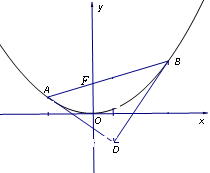
(1) 求点 的纵坐标;
的纵坐标;
(2) 证明: 、
、 、
、 三点共线;
三点共线;
(1) -1;(2)只需证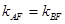 。
。
解析试题分析:(1)设点 、
、 的坐标分别为
的坐标分别为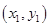 、
、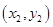 ,
,
∵ 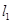 、
、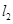 分别是抛物线
分别是抛物线 在点
在点 、
、 处的切线,
处的切线,
∴直线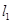 的斜率
的斜率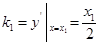 ,直线
,直线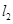 的斜率
的斜率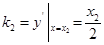 .
.
∵ 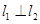 , ∴
, ∴ 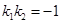 , 得
, 得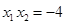 . ① 3分
. ① 3分
∵ 、
、 是抛物线
是抛物线 上的点,
上的点,
∴ 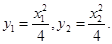
∴ 直线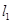 的方程为
的方程为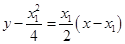 ,直线
,直线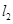 的方程为
的方程为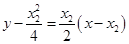 .
.
由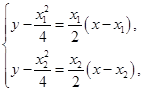 解得
解得
∴点 的纵坐标为
的纵坐标为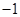 . 6分
. 6分
(2) 证法1:∵  为抛物线
为抛物线 的焦点, ∴
的焦点, ∴ 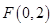 .
.
∴ 直线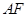 的斜率为
的斜率为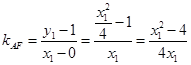 ,
,
直线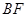 的斜率为
的斜率为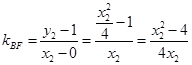 .
.
∵ 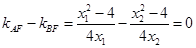 9分
9分
∴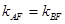 .
.
∴ 、
、 、
、 三点共线. 13分
三点共线. 13分
证法2:∵  为抛物线
为抛物线 的焦点,
的焦点,
∴ 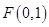 . ∴
. ∴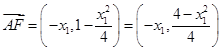 ,
, .
.
∵ 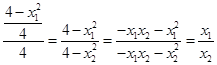 , 9分
, 9分
∴ 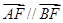 .
.
∴ 、
、 、
、 三点共线. 13分
三点共线. 13分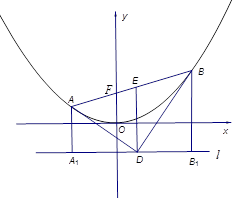
考点:直线与抛物线的综合应用;向量关系的性质;直线垂直的条件;三点共线的证明;
点评:向量法证明三点共线的常用方法:
(1)若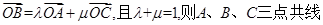 ;
;
(2)若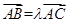 ,则A、B、C三点共线。
,则A、B、C三点共线。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
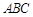 的两个顶点
的两个顶点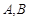 的坐标分别是
的坐标分别是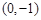 ,
,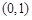 ,且
,且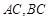 所在直线的斜率之积等于
所在直线的斜率之积等于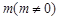 .
.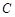 的轨迹
的轨迹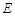 的方程,并判断轨迹
的方程,并判断轨迹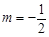 时,过点
时,过点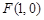 的直线
的直线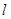 交曲线
交曲线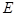 于
于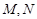 两点,设点
两点,设点 关于
关于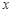 轴的对称点为
轴的对称点为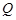 (
(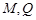 不重合).求证直线
不重合).求证直线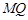 与
与 ,
, 是抛物线
是抛物线 上相异两点,且满足
上相异两点,且满足 .
. 的中垂线经过点
的中垂线经过点 ,求直线
,求直线 轴于点
轴于点 ,求
,求 的面积的最大值及此时直线
的面积的最大值及此时直线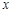 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)  平行于
平行于 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.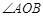 为钝角,求直线
为钝角,求直线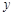 轴上的截距m的取值范围;
轴上的截距m的取值范围; 、
、 分别是椭圆
分别是椭圆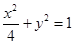 的左、右焦点。
的左、右焦点。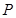 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点,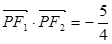 ,求点P的坐标;
,求点P的坐标; 与椭圆交于不同的两点A、B,且
与椭圆交于不同的两点A、B,且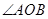 为锐角(其中
为锐角(其中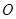 为坐标原点),求直线
为坐标原点),求直线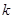 的取值范围。
的取值范围。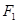
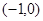 、
、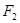
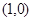 为椭圆的焦点,且直线
为椭圆的焦点,且直线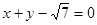 与椭圆相切.
与椭圆相切. 、
、 两点,求△
两点,求△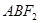 的面积
的面积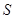 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: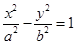 的一个焦点
的一个焦点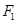 且垂直于
且垂直于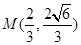 .
.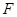 的坐标;
的坐标;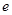 .
.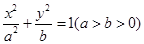 的左、右焦点分别为
的左、右焦点分别为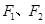 ,离心率
,离心率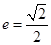 ,
, 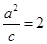 .
.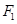 的直线
的直线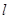 与该椭圆交于
与该椭圆交于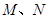 两点,且
两点,且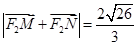 ,求直线
,求直线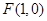 ,直线
,直线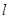 :
: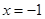 交
交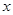 轴于点
轴于点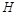 ,点
,点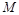 是
是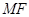 的垂直平分线交于点
的垂直平分线交于点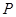 .
.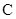 的方程;(Ⅱ)若 A、B为轨迹
的方程;(Ⅱ)若 A、B为轨迹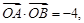 证明直线AB必过一定点,并求出该定点.
证明直线AB必过一定点,并求出该定点.