已知向量$\overrightarrow{a}$=(1.2).$\overrightarrow{b}$=.且$\overrightarrow{a}$⊥$\overrightarrow{b}$.则x的值为$-\frac{1}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

5．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（1+x，x），且$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x的值为$-\frac{1}{3}$．

分析由$\overrightarrow{a}$⊥$\overrightarrow{b}$，可得$\overrightarrow{a}$•$\overrightarrow{b}$=0，即可得出．

解答解：∵$\overrightarrow{a}$⊥$\overrightarrow{b}$，
∴$\overrightarrow{a}$•$\overrightarrow{b}$=（1+x）+2x=1+3x=0，
解得x=$-\frac{1}{3}$，
故答案为：-$\frac{1}{3}$．

点评本题考查了向量垂直与数量积的关系，考查了推理能力与计算能力，属于中档题．

练习册系列答案

16．如图的程序框图表示算法的运行结果是（　　）

13．

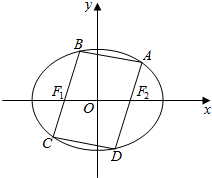如图，已知四边形ABCD是椭圆3x²+4y²=12的内接平行四边形，且BC，AD分别经过椭圆的焦点F₁，F₂．
（Ⅰ）若直线AC的方程为x-2y=0，求AC的长；
（Ⅱ）求平行四边形ABCD面积的最大值．

20．设空间直角坐标系中A（1，0，0），B（0，1，0），C（1，1，0），则点P（x，y，3）到平面ABC的距离是（　　）

10．若直线（a+1）x+2y=0与直线x-ay=1互相垂直，则实数a的值等于（　　）

17．若4≤a≤8，0≤b≤2，则a+b的取值范围是（　　）

14．椭圆$\frac{x^2}{2}+{y^2}$=1上一点P到右焦点的距离为$\frac{{\sqrt{2}}}{2}$，则点P到左准线的距离为3．

15．

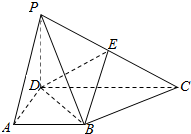在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=2，CD=4．
（1）求证：BC⊥平面PBD；
（2）设E是侧棱PC上一点，且CE=2PE，求四面体P-BDE的体积．

试题分类