题目内容
11．已知点P是边长为2的正方形内任一点，则点P到四个顶点的距离均大于1的概率是（ ）| A． | $\frac{π}{4}$ | B． | $\frac{4-π}{4}$ | C． | $\frac{1}{4}$ | D． | $\frac{π}{3}$ |
分析 根据题意，先求出满足条件的正方形的面积，再求出满足条件正方形内的点到正方形的顶点的距离均大于1的图形的面积，然后代入几何概型公式即可得到答案．
解答 解：满足条件的正方形的面积S正方形=2×2=4；
满足点P到四个顶点的距离均大于1的面积S=4-π，
故点P到四个顶点的距离均大于1的概率是P=$\frac{4-π}{4}$；
故选：B．
点评 本题考查几何概型，解题的关键理解几何概型的意义，即将长度、面积、体积的比值转化为事件发生的概率．
练习册系列答案
名校课堂系列答案
相关题目
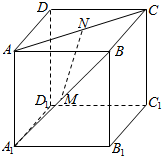如图所示，在正方体ABCD-A1B1C1D1中，棱长为a，M、N分别是棱A1B、AC上的点，A1M=AN．
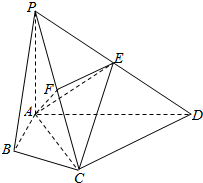在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2AB=4．
19．已知A（2，-5，1），B（1，-4，1），C（2，-2，4），则$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
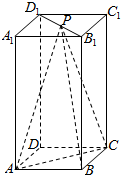如图所示，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=4，P为线段B1D1上一点．
的图象向右平移
个单位后与
的图象重合，则
_________．