题目内容
16.在空间直角坐标系Oxyz中,y釉上有一点M到已知点A(4,3,2)和B(2,5,2)的距离相等,则点M的坐标是(0,1,0).分析 根据题意,设出y轴上的点M的坐标,利用|MA|=|MB|,列出方程求出点M的坐标.
解答 解:设y轴上的点M(0,y,0),则|MA|=|MB|,
即42+(3-y)2+22=22+(5-y)2+22,
解得y=1,
所以点M(0,1,0).
故答案为:(0,1,0).
点评 本题考查了求空间直角坐标系中两点间的距离的应用问题,是基础题目.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
6.平面内有一长度为4的线段AB,动点P满足|PA|+|PB|=6,则点P的轨迹是( )
| A. | 直线 | B. | 射线 | C. | 椭圆 | D. | 双曲线 |
11.设集合 U={1,2,3,4,5,6},A={1,2,3},B={2,5},则A∩(∁UB)=( )
| A. | {1,3 } | B. | { 2 } | C. | {2,3} | D. | { 3 } |
6.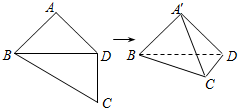 如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )
如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )
 如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )
如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )| A. | A′B⊥CD | |
| B. | 四面体A′BCD的体积为$\frac{1}{2}$ | |
| C. | A′C与BD所成的角为60° | |
| D. | 四面体A′BCD的外接球的表面积为$\frac{7π}{2}$ |
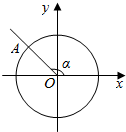 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为$\frac{2}{3}$,则cosα=-$\frac{\sqrt{5}}{3}$.
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为$\frac{2}{3}$,则cosα=-$\frac{\sqrt{5}}{3}$.