题目内容
8．绝对值不等式|x+1|＜0的解集∅．分析 由绝对值的意义，不等式|x+1|＜0等价于$\left\{\begin{array}{l}{x+1≥0}\\{x+1＜0}\end{array}\right.$①或$\left\{\begin{array}{l}{x+1＜0}\\{-（x+1）＜0}\end{array}\right.$②，分别解不等式组取并集即可得答案．
解答 解：根据题意，不等式|x+1|＜0等价于$\left\{\begin{array}{l}{x+1≥0}\\{x+1＜0}\end{array}\right.$①或$\left\{\begin{array}{l}{x+1＜0}\\{-（x+1）＜0}\end{array}\right.$②，
解可得①、②均是空集，
则不等式|x+1|＜0的解集为∅；
故答案为：∅．
点评 本题考查绝对值不等式的解法，属于基本的题目．
练习册系列答案
相关题目
19．
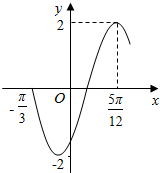函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则这个函数的周期和初相分别是（ ）
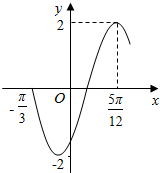函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则这个函数的周期和初相分别是（ ）| A． | 2，-$\frac{π}{3}$ | B． | 2，-$\frac{π}{6}$ | C． | π，-$\frac{π}{6}$ | D． | π，-$\frac{π}{3}$ |
3．已知a＜b，则下列各式正确的是（ ）
| A． | a2＜b2 | B． | ac＜bc | C． | log2a＜log2b | D． | 2a＜2b |
13．已知函数f（x）对任意x∈R，都有f′（x）+f（x）≤0成立，其中f′（x）为f（x）的导函数，则（ ）
| A． | 3f（ln3）＜ef（1） | B． | 3f（ln3）≤ef（1） | C． | 3f（ln3）＞ef（1） | D． | 3f（ln3）≥ef（1） |